How to plot the transmission coefficient as a function of #E//V_0#?
1 Answer
Here is the Excel sheet I made while doing this.
Here we follow what is readily found in McQuarrie & Simon (pp. 142-143). We found that:
#T = {([1 + [sinh^2[v_0^(1//2)(1 - r)^(1//2)]]/(4r(1 - r))]^(-1),0 < r < 1),([1 + [sin^2[v_0^(1//2)(r - 1)^(1//2)]]/(4r(r - 1))]^(-1),r >= 1):}# where:
#T# is the transmission coefficient (i.e. the fraction of particles that tunnel).#r = E/V_0 = epsilon/v_0# is the ratio of the particle energy to the barrier height.#v_0 = (2ma^2V_0)/ℏ^2# is a unitless variable for the height of the barrier.#epsilon = (2ma^2E)/ℏ^2# is a unitless variable for the energy of the particle.
and because I thought it would be interesting, besides
It is rather interesting that the higher the barrier gets, the more values of
#ul(V_0" "" "" "" "" "E//V_0" "" "" "%T" ")#
#10ℏ^2//2ma^2" "color(white)(.)1.99" "" "" "" "100%#
#" "" "" "" "" "" "4.95#
#20ℏ^2//2ma^2" "color(white)(.)1.49" "" "" "" "#
#" "" "" "" "" "" "2.97#
#40ℏ^2//2ma^2" "color(white)(.)1.25" "" "" "" "#
#" "" "" "" "" "" "1.99#
#" "" "" "" "" "" "3.22#
#" "" "" "" "" "" "4.95#
It just so happens that at the classical limit, we have
#lim_(V_0 -> oo) T = 100%# for#E > V_0# ,
with a rigid cutoff at
DISCLAIMER: LONG AND RIGOROUS DERIVATION!
The potential is set up as:
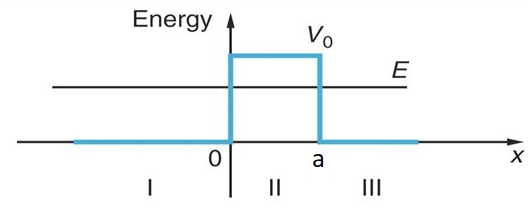
#V(x) = {(0, x < 0),(V_0, 0 < x < a),(0, x > a):}#
We of course set
#psi_I(x) = Ae^(ikx) + Be^(-ikx), " "x < 0#
#psi_(II)(x) = Ce^(k'x) + De^(-k'x), " "0 < x < a#
#psi_(III)(x) = Fe^(ikx) + Ge^(-ikx), " "x > a# where
#k = sqrt((2mE)/ℏ^2)# and#k' = sqrt((2m(V_0 - E))/ℏ^2)# .
If we restrict the particle to only come in from the left,
#T = (|F|^2)/(|A|^2)#
The continuity conditions are:
#ul(psi_I(0) = psi_(II)(0))# :
#A + B = C + D# #" "" "" "" "" "" "bb((1))#
#ul((dpsi_I(0))/(dx) = (dpsi_(II)(0))/(dx))# :
#ik(A - B) = k'(C - D)# #" "" "" "bb((2))#
#ul(psi_(II)(a) = psi_(III)(a))# :
#Ce^(k'a) + De^(-k'a) = Fe^(ika)# #" "" "" "bb((3))#
#ul((dpsi_(II)(a))/(dx) = (dpsi_(III)(a))/(dx))# :
#k'Ce^(k'a) - k'De^(-k'a) = ikFe^(ika)# #" "bb((4))#
Now, we take
#color(green)(2ikA = (ik + k')C + (ik - k')D)#
Then, take
#2k'Ce^(k'a) = (k' + ik)Fe^(ika)#
#color(green)(C = ((k' + ik)/(2k'))Fe^(ika)e^(-k'a))#
and take
#2k'De^(-k'a) = (k' - ik)Fe^(ika)#
#color(green)(D = ((k' - ik)/(2k'))Fe^(ika)e^(k'a))#
Plug it back into the first result to get:
#2ikA = (ik + k')((k' + ik)/(2k'))Fe^(ika)e^(-k'a) + (ik - k')((k' - ik)/(2k'))Fe^(ika)e^(k'a)#
#= [(ik - k')(k' - ik)e^(k'a) + (ik + k')(k' + ik)e^(-k'a)] (Fe^(ika))/(2k')#
#= [(k^2 - k'^2 + 2ikk')e^(k'a) + (k'^2 - k^2 + 2ikk')e^(-k'a)] (Fe^(ika))/(2k')#
#= [(k^2 - k'^2)(e^(k'a) - e^(-k'a)) + 2ikk'(e^(k'a) + e^(-k'a))] (Fe^(ika))/(2k')#
Now, we use the identities
#2ikA = [2(k^2 - k'^2)sinh(k'a) + 4ikk'cosh(k'a)] (Fe^(ika))/(2k')#
Solve for
#F/A = (2ik)/{[2(k^2 - k'^2)sinh(k'a) + 4ikk'cosh(k'a)]e^(ika)/(2k')}#
#= (4ikk'e^(-ika))/[2(k^2 - k'^2)sinh(k'a) + 4ikk'cosh(k'a)]#
Using the definition of
#T -= (F^"*"F)/(A^"*"A) = [(4ikk'e^(-ika))/[2(k^2 - k'^2)sinh(k'a) + 4ikk'cosh(k'a)]]^"*" [(4ikk'e^(-ika))/[2(k^2 - k'^2)sinh(k'a) + 4ikk'cosh(k'a)]]#
# = (4k^2k'^2)/((k^2 - k'^2)^2sinh^2(k'a) + 4k^2k'^2cosh^2(k'a))#
Next, use the identity that
#T = (4k^2k'^2)/((k^2 - k'^2)^2sinh^2(k'a) + 4k^2k'^2 + 4k^2k'^2sinh^2(k'a))#
#= (4)/(4 + (k^2 - k'^2)^2/(k^2k'^2)sinh^2(k'a) + 4sinh^2(k'a))#
#= (4)/(4 + (k^4 - 2k^2k'^2 + k'^4)/(k^2k'^2)sinh^2(k'a) + (4k^2k'^2)/(k^2k'^2) sinh^2(k'a))#
#= (4)/(4 + (k^4 + 2k^2k'^2 + k'^4)/(k^2k'^2)sinh^2(k'a))#
#= (4)/(4 + (k^2 + k'^2)^2/(k^2k'^2)sinh^2(k'a))#
Then, insert
#T = (4)/(4 + ((2mV_0)/ℏ^2)^2/(((2m)/ℏ^2)^2 E(V_0 - E))sinh^2(sqrt((2ma^2(V_0 - E))/ℏ^2)))#
#= 4/(4 + (V_0^2)/(E(V_0 - E))sinh^2(sqrt((2ma^2(V_0 - E))/ℏ^2)))#
Now, let the unitless quantities
#V_0 = (ℏ^2v_0)/(2ma^2)# ,#" "E = (ℏ^2epsilon)/(2ma^2)#
and we then rewrite
#T = 4/(4 + (((ℏ^2)/(2ma^2))^2v_0^2)/((ℏ^2epsilon)/(2ma^2)((ℏ^2v_0)/(2ma^2) - (ℏ^2epsilon)/(2ma^2)))sinh^2(sqrt(v_0 - epsilon)))#
#= 4/(4 + (cancel(((ℏ^2)/(2ma^2))^2)v_0^2)/(cancel(((ℏ^2)/(2ma^2))^2) epsilon(v_0 - epsilon))sinh^2(sqrt(v_0 - epsilon)))#
#= 1/(1 + (v_0^2)/(4epsilon(v_0 - epsilon))sinh^2(sqrt(v_0 - epsilon)))#
Finally, let
#T = 1/(1 + cancel(v_0^2)/((4epsilon)/v_0 cancel(v_0^2)(1 - r))sinh^2(sqrt(v_0(1 - r))))#
#= barul|" "1/(1 + [sinh^2[v_0^(1//2)(1 - r)^(1//2)]]/(4r(1 - r)))" "|#
Now, when we plot this, if we want
#color(blue)(T = {([1 + [sinh^2[v_0^(1//2)(1 - r)^(1//2)]]/(4r(1 - r))]^(-1),0 < r < 1),([1 + [sin^2[v_0^(1//2)(r - 1)^(1//2)]]/(4r(r - 1))]^(-1),r >= 1):})#
Let's choose

