How to solve inclined plane questions?

Can someone please explain to me how to do question 2? Thanks!

Can someone please explain to me how to do question 2? Thanks!
1 Answer
Explanation:
Funnily enough, this is not actually a force problem at all, as you might think. It's a conservation of energy problem.
Let's set up a diagram for this:
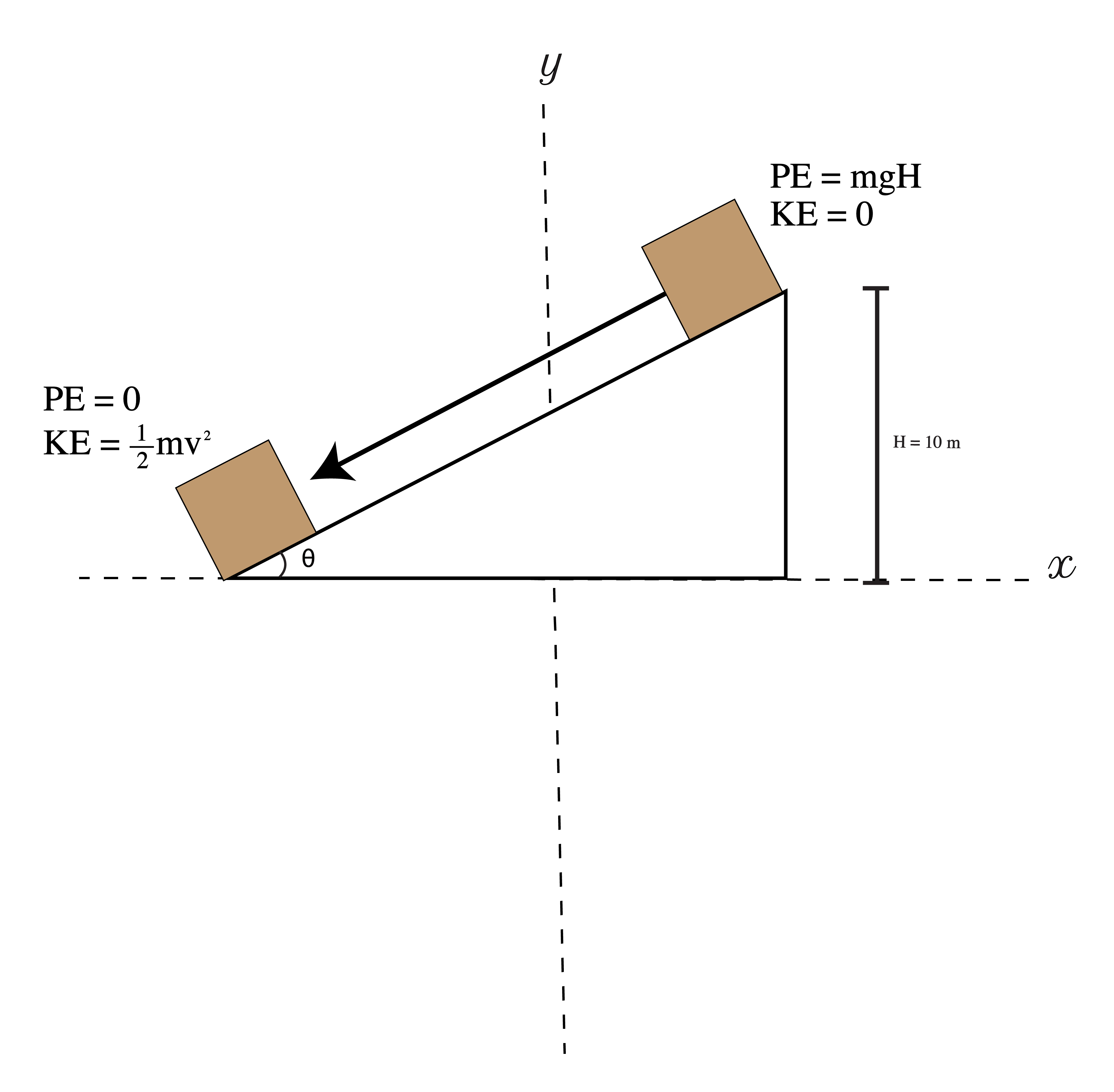 By Darshan Senthil
By Darshan Senthil
So, you can set up a conservation of energy equation:
Now, you plug in everything from he diagram. Notice that
Notice that mass cancels out:
Now, all you do is solve for
How would velocity vary if the mass were different? Well, look back, and recall that mass cancels out. Hence, ideally, the velocity would not change with mass! So whether you have an ant, a tennis ball, an elephant, or even a Soviet Tank, it would have a velocity of 14 m/s if it were sliding down a frictionless slope.
The reason this doesn't happen in real life is because there is usually friction involved, and the strength of friction is proportional to normal force, which increases with mass.
Hope that helped :)

