Question

How to solve the equation `z^4=ibarz` ? Where z is a complex number.

Answer 1

`S = { 0, e^((ipi)/10) }`

Explanation:

Let's think of these complex numbers in exponential forms!

`z` is a complex number of phase, or angle `theta`, and its conjugate has the angle `-theta`, we can see that by algebra if we use certain trig properties (the cosine is even and the sine is odd):

`z = re^(itheta) = cos(theta) + i*sin(theta) = a + bi`
`barz = re^(-itheta) = cos(-theta) + isin(-theta) = cos(theta) -isin(theta) = a -bi`

So, rewriting this in terms of angles, we have:

`re^(i*4theta) = i*re^(-itheta)`

Remembering that `i` also has an exponential form, `e^(pi/2*i)`

`re^(i*4theta) = re^(i(pi/2-theta))`
`i*4theta = i(pi/2 - theta)`
`4theta = pi/2 - theta`
`5theta = pi/2`
`theta = pi/10`

Now to solve for the radius, we know that:

`z^4 = ibarz`

By taking the absolute value of both sides we have

`|z^4| = |ibarz|`

Which we can split

`|z|^4 = |i||barz|`

But `|z| = |barz|` and it's defined as the radius we want to discover, so

`r^4 = |i|*r`

`|i| = 1`, so simplifying we have

`r^4 = r`

There are only two real numbers (remember that the absolute value / radius is always real) that can satisfy this equation

`r = 1` or `r = 0`

Answer 2

`z=0,i`
`z = +-1/2sqrt(1/2(5+sqrt(5))) + 1/4(sqrt(5)-1)i`
`z = +-1/2sqrt(1/2(5-sqrt(5))) - 1/4(sqrt(5)+1)i`

Explanation:

We have:

`z^4 = i barz`,

Where `barz` is the complex conjugate of `z`

If we use the exponential form of a complex number then we can represent the solution by;

`z= re^(itheta) \ \ \ (=rcostheta+irsintheta)`

Then the complex conjugate will be:

`z= re^(-itheta)`

Whenever dealing with complex equation such as this it is essential to remember that the complex exponential has a period of `2pi`, and thus we can modify the conjugate, and substitute into the equation to solve to get;

`{re^(itheta)}^4 = i(re^(-itheta))`
`{re^(itheta)}^4 = i(re^(i(-theta+2npi)))` where `n in NN`

(Equally we could have incorporated this periodicity into the RHS exponent, it really does not matter providing it is incorporated somewhere). Replacing `i` by its complex exponential form `i=e^(ipi/2)` we get:

`{re^(itheta)}^4 = e^(ipi/2)(re^(i(-theta+2npi)))`
`:. r^4e^(4itheta) = re^(i(pi/2-theta+2npi))`

Equating real and imaginary terms (or the moduli and arguments) we have:

`Re\ : \ \ r^4=r`
`Im: \ \ 4theta = pi/2-theta +2npi`

From the first equation we get:

`r^4-r = 0`
`:. r(r^3-1) = 0`
`:. r=0,1`

From the second equation we get:

`4theta = pi/2-theta +2npi`
`:. 5theta = pi/2 +4npi/2`
`:. theta = (4n+1)pi/10`

So now we can "assemble" the solutions:

`r= 0=> z=0`

`r= 1=> z=e^(itheta)`

And By putting `n=0,1,2,3,...` we get:

`theta = (pi)/10, pi/2, (9pi)/10, (13pi)/10, (17pi)/10, ...`

And with these values of `theta`, and using `z=costheta + isintheta` we get:

`n=0: => z = 1/2sqrt(1/2(5+sqrt(5))) + 1/4(sqrt(5)-1)i`
`n=1: => z = 0 + 1i`
`n=2: => z = -1/2sqrt(1/2(5+sqrt(5))) + 1/4(sqrt(5)-1)i`
`n=3: => z = -1/2sqrt(1/2(5-sqrt(5))) - 1/4(sqrt(5)+1)i`
`n=4: => z = 1/2sqrt(1/2(5-sqrt(5))) - 1/4(sqrt(5)+1)i`

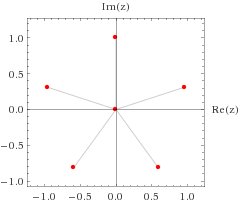
After which the pattern repeats. Hence there are six solutions:

`z=0,i`
`z = +-1/2sqrt(1/2(5+sqrt(5))) + 1/4(sqrt(5)-1)i`
`z = +-1/2sqrt(1/2(5-sqrt(5))) - 1/4(sqrt(5)+1)i`
We can see these solutions on the Argand diagram: