How to Solve These Basic Trigonometry Questions (Bearings, Word Problems)?
Hi All,
I know you are all busy, but I don't understand how to solve these, please help? Please fully answer all parts of the question, thank you!
Question #5

Question #18 and # 19

Question #3 and # 4
Hi All,
I know you are all busy, but I don't understand how to solve these, please help? Please fully answer all parts of the question, thank you!
Question #5

Question

Question

2 Answers
Question 5
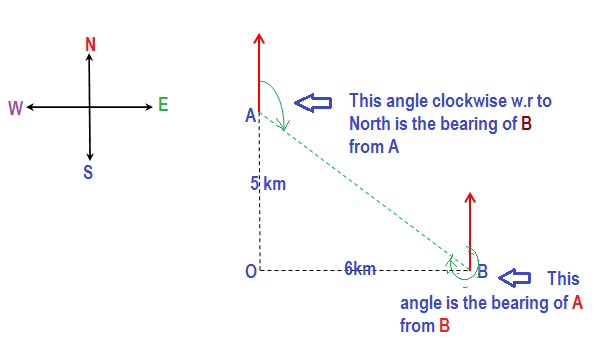
In the above figure O is the starting point. A and B are the positions of two runners after 30 min or 0.5hour running @ 10km/h towards north and @12km/h towards east respectively.
So
By Pythagorean theorem
The distance of runner B from A
Bearing is always measured in clockwise direction w.r. to north line (shown in figure by red arrow)
So the bearing of B from A
Question 18
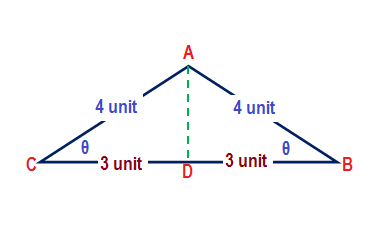
The given triangle is isosceles in which the equal sides are
It is obvious from figure that
So
Question 19
As per given condition of the question the second isosceles triangle (EBC) has same base that of first one (ABC) but the area of second one is thrice that of first one. It is possible only if the height of second triangle is thrice that of first one. Since the area of the triangle is proportional to height when base is constant.
This has been shown in the fig below.
The perpendicular drawn from vertex of an isosceles triangle bisects the base.
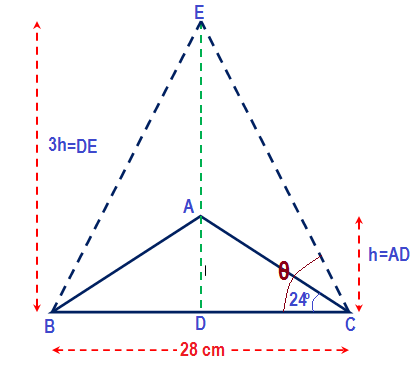
From fig
Now
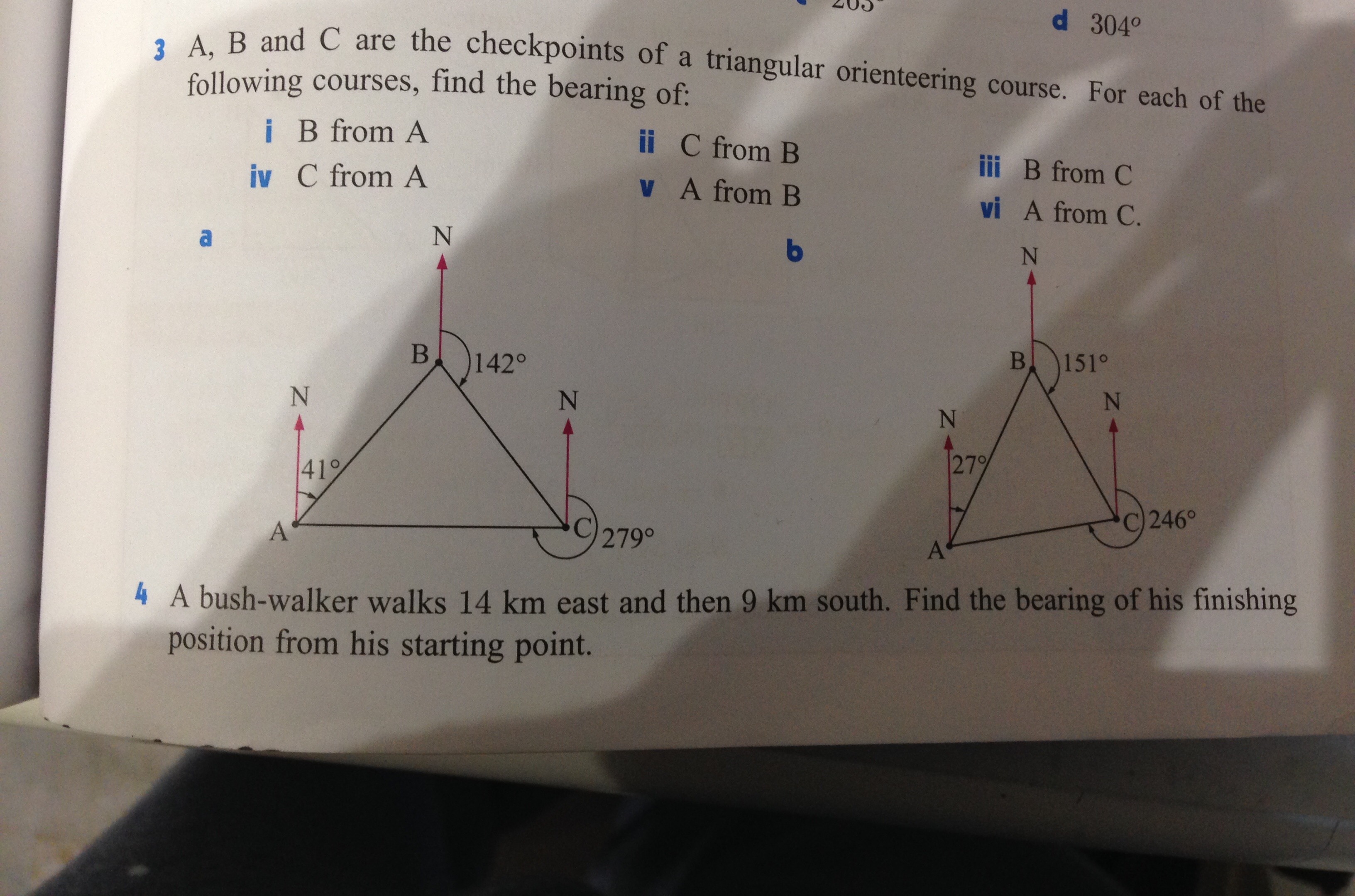
Question 3a
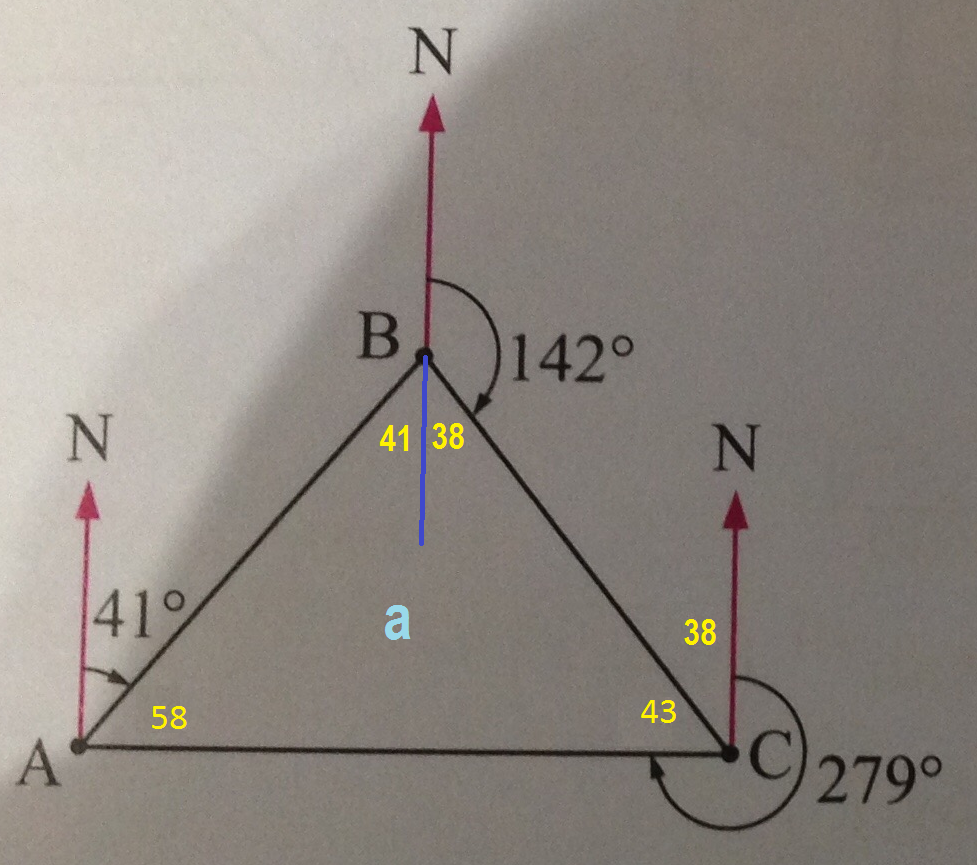
Bearing
I)
II)
III)
IV)
V)
VI)
Question 3b
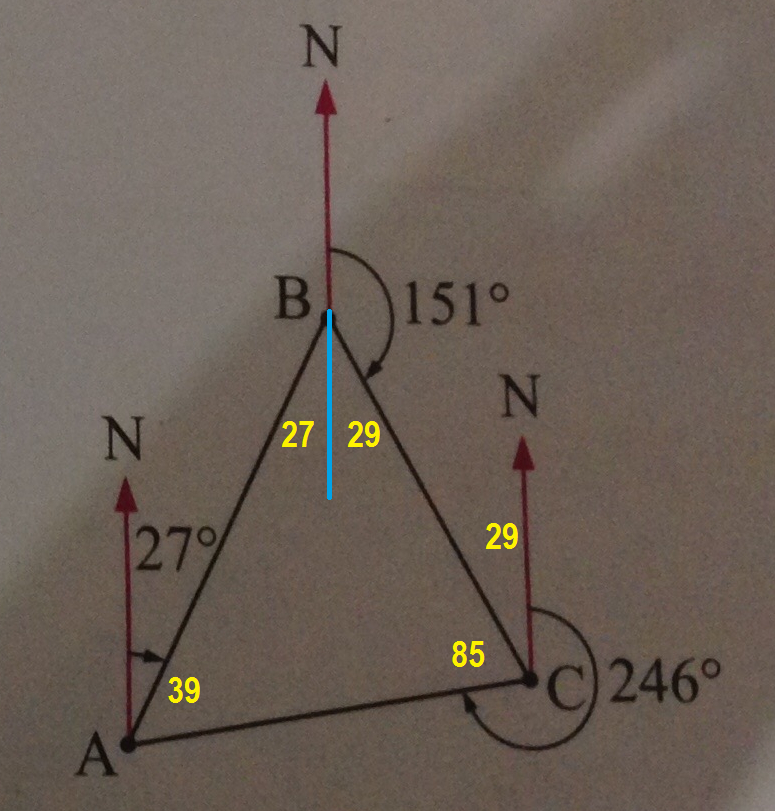
Bearing
I)
II)
III)
IV)
V)
VI)
Question 4
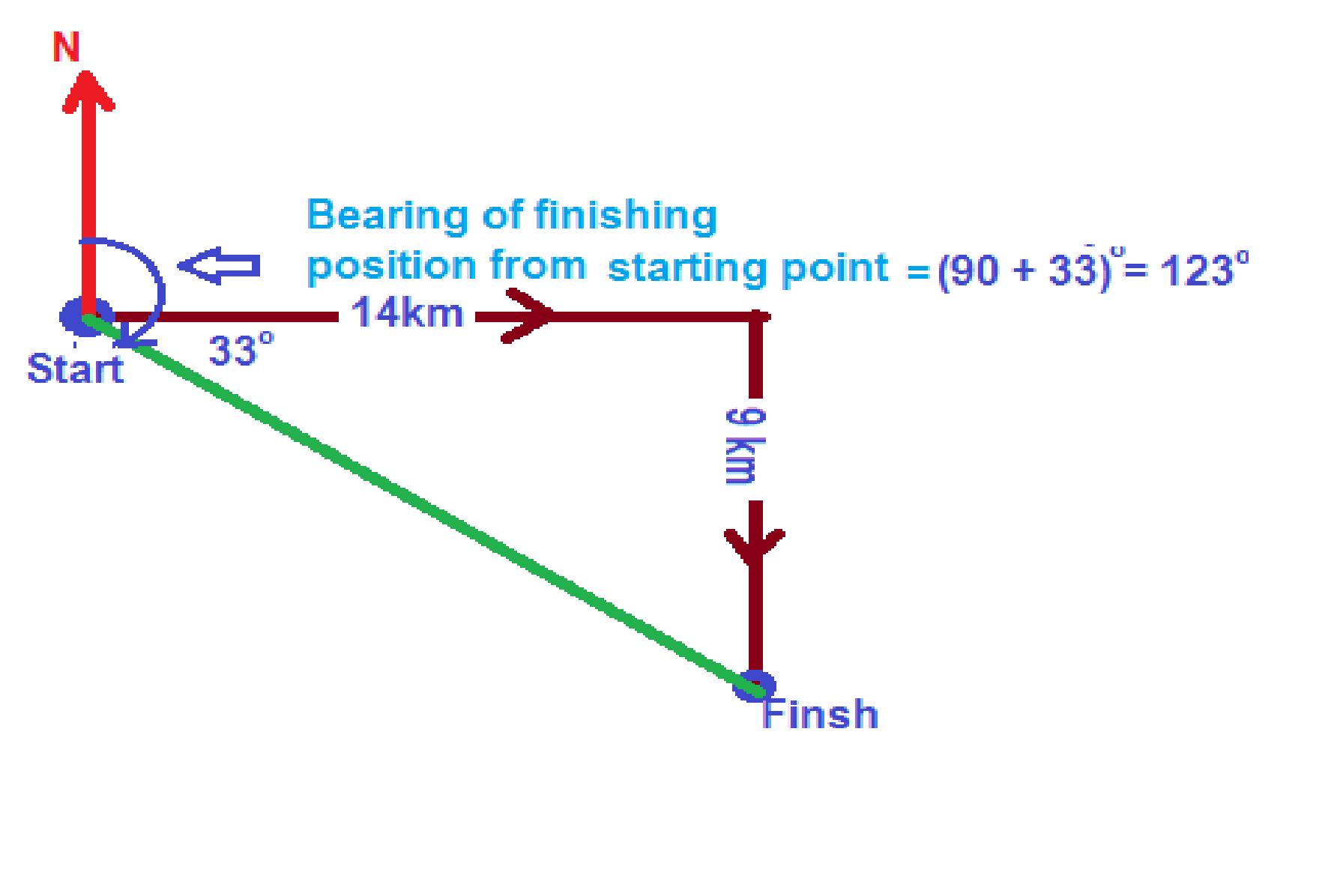
Bearing =
5.
19,
Explanation:
- Let A and B start from O.
After half an hour,
- Let the base be BC = b and equal sides AB = AC = a.
Then the equal sides length
#cos (base angle) = cos B =(b/2)/a=3/4.
So,
- Let the altitude be AN and base BC.
In
tan B = AN/BN=AN/14.
So, the altitude AN = 14 tan B=14 tan 24^o#.
Treble this area =588tan24^o.
For this area,
the corresponding same-base base angle B is given by
So,
For this approximation, I have used calculator

