How to solve this question?
 Screenshot
Screenshot
 Screenshot
Screenshot
4 Answers
a) Not answer
b) not answered
c)
d)
Read disclaimer
Explanation:
Disclaimer: I'm fairly sure my method is not that expected from the question, but I found it interesting and wanted to share my attempt anyway. I think its wrong because I effectively skipped parts a and b. Any feedback on this would be great!
Assumptions I've made which might be wrong:
- all the energy transferred in the spring is transferred into kinetic energy for the marble and piston when the piston returns to equilibrium
- the marble and piston travel together as a single particle until the piston returns to equilibrium piston, then the marble is projected off.
Consider the problem in stages.
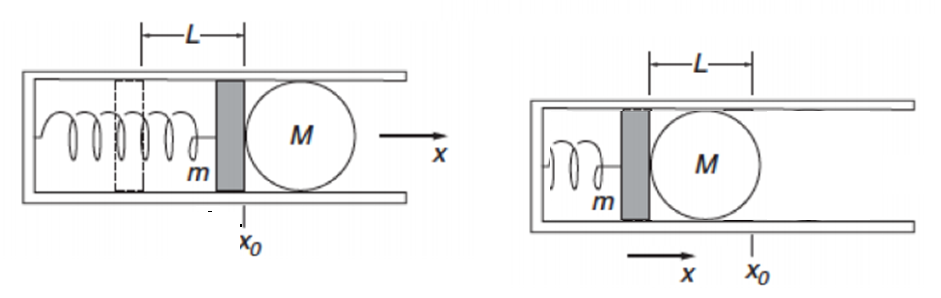
Due to the conservation of energy, this will all be transformed to kinetic energy when the piston returns to
This is the kinetic energy possessed by the whole system, this being the piston and marble.
Let
Now, consider when the marble slips from the piston.
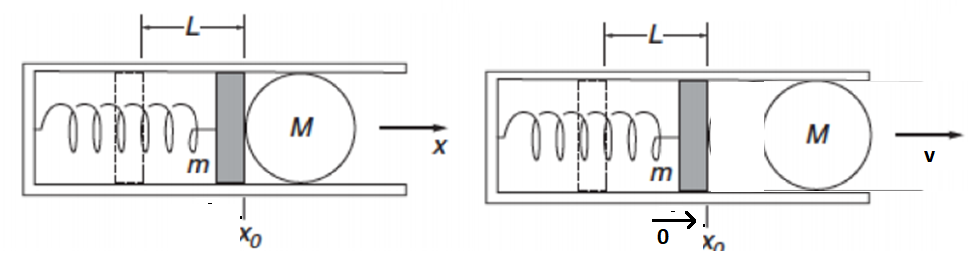
The piston will be stationary at the end, so has a final velocity of 0.
We can find the final speed of the marble using the conservation of momentum.
From conservation of momentum
Total momentum before = total momentum after
for part d), we will do the inverse.
Let the marble be projected off at speed
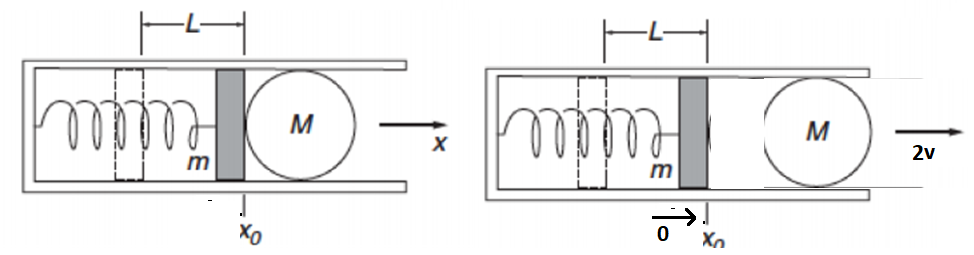
From conservation of momentum
Momentum before=momentum after
Now, we'll use our energy idea from earlier to find our new length back for the spring,
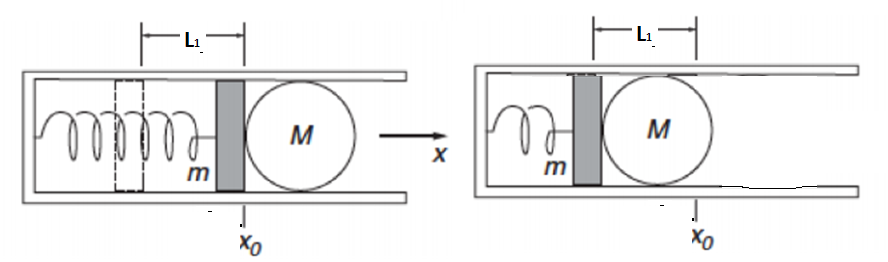
By conservation of energy;
So to get double the speed out, double the distance you pull the spring. (rather boring final answer, if I do say so).
See below.
Explanation:
Movement equation
Multiplying by
Calling
this relationship works just until the marble loses contact with the piston.
Also integrating directly the movement equation
which is a harmonic movement equation results
and
See parts (c) and (d) as a separate answer.
Explanation:
(a) Keeping in view the given figure, and considering
F_"net"=(M+m)(d^2x)/dt^2=-kx
Rewriting it as a second order differential equation of SHM.
(d^2x)/dt^2+(k)/(M+m)x=0 ......(1)
(b) Above equation has a general sinusoidal solution as
x=Asin\ omegat+B cos\ omega t ......(2)
whereomega=sqrt((k)/(M+m))
Now velocity is given by
dot x=omegaAcosomegat-omegaBsinomegat ......(3)
Displacement at
-L=Asin\ (omegaxx0)+B cos\ (omega xx0)
=>B=-L
Velocity at
0=omegaAcos(omegaxx0)-omegaBsin(omegaxx0)
=>A=0
Solution (2) becomes
x=-L cos\ omega t
Velocity becomes
dot x=omegaLsinomegat
It is clear that equation of motion and its solution are valid so long as piston and marble move together as single entity.
From other posted solution we got
Position
x=-L cos\ omega t ......(i)
Velocity
dot x=omegaLsinomegat ........(ii)
Explanation:
(c) Let velocity of the piston marble system be maximum at
sinomegaT=1
=>omegaT=pi/2
dotx_max=omegaL
=>dotx_max=sqrt(k/(m+M))L ......(iii)
Inserting value of
x(T)=-L cos\ (pi/2)
x(T)=0=x_0
(d) From
dot x_maxpropL
Therefore, in order to achieve twice the speed of marble on separation the piston must be pushed/pulled back twice the initial value.
=2L

