How to solve worded quadratic problems?
can someone please explain to me how to do question 2c)? Thank you so much!
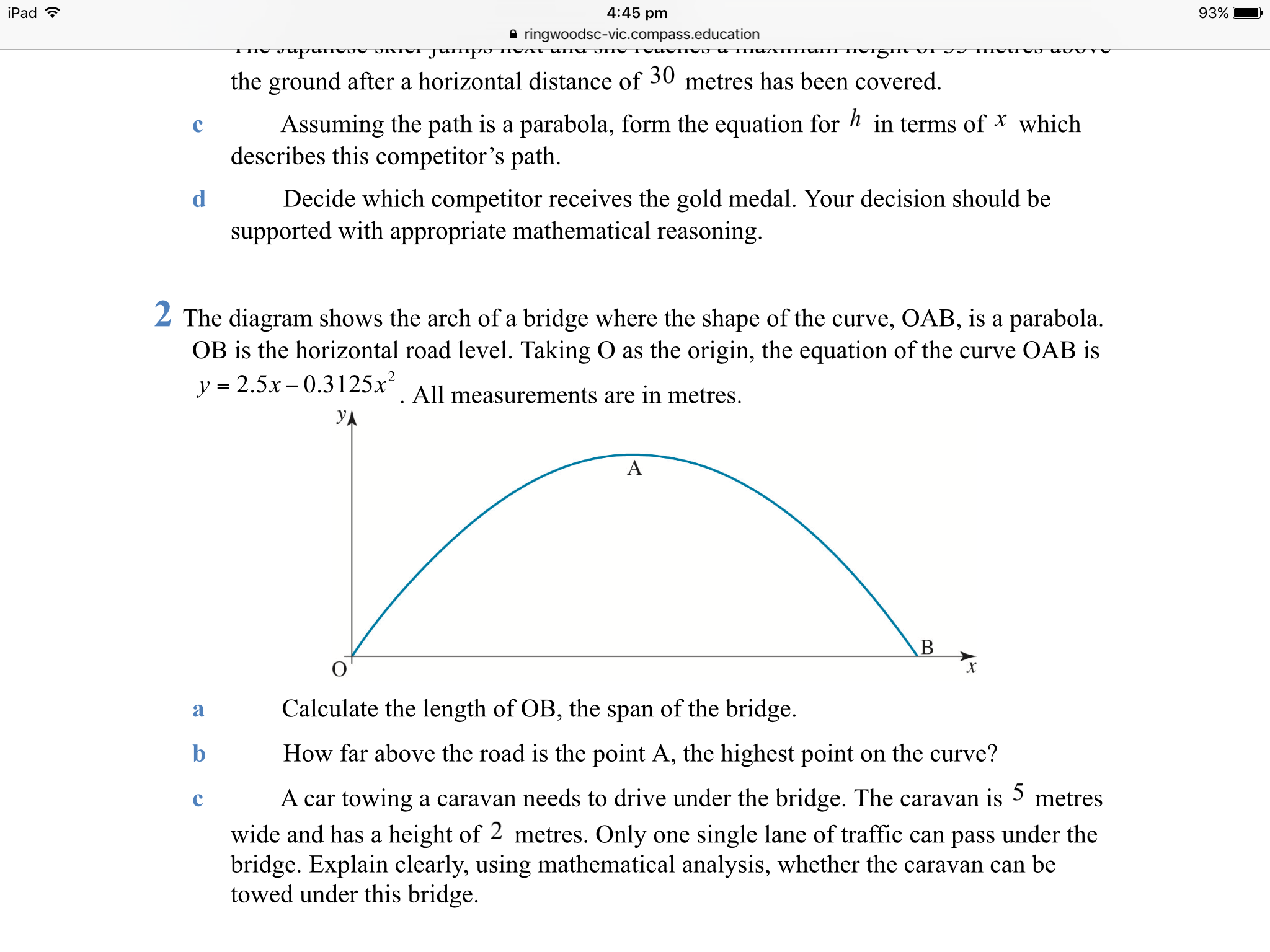
can someone please explain to me how to do question 2c)? Thank you so much!
1 Answer
Answering question part 2c
Yes! The tcaravan will fit.
Explanation:
Set y to the value of 2 (height of caravan ) and calculate the horizontal distance between the points of the curve at that height (
Subtract 2 from both sides giving
Now solve as a quadratic.
Given the standardised form of:
Once you have the difference between the two values of
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
So at the caravan's height of 2 meters the x-coordinates are:
As we have
The trailer is 5 metres wide so this will fit that gap with an approximate total sideways clearance of 4.3 metres.
Approximately 2.15 metres clearance either side

