Question

How will you answer this?

A particle moving in a straight line has a velocity of `v" " ms^-1` such that, t seconds after leaving a fixed point, `v = 4t^2 - 8t + 3`.

Find the total distance the particle has travelled when t=1.5.

Answer 1

`4/3`[m]

Explanation:

Observing the `v xx t` graphics,

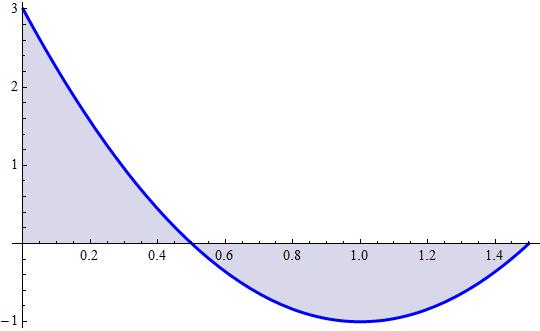
we know that the area represents the distance. In the graphics, the positive area and the negative area are equal so the movement is a movement that returns to the initial position after having attained a distance `d` from the origin or a movement with null displacement. The distance is then `2d` instead `d-d`

Now equating `v = 4t^2-8t+3=4(t-1/2)(t-3/2)` then

`2d = int_0^(1/2)(4t^2-8t+3)dt -int_(1/2)^(3/2)(4t^2-8t+3)dt = 2/3-(-2/3)=4/3`[m]