How will you prove the trigonometric formula #cos(A+B)=cosAcosB-sinAsinB# by using formula of cross product of two vectors ?
2 Answers
I could prove it using the dot product of vectors.
Explanation:
Let
The unit vectors can be written in Cartesian form as
To prove
We know that dot product of two vectors is
Inserting our unit vectors in the above;
Using equation (1)
LHS
From property of dot product we know that only terms containing
Equating LHS with RHS we obtain
As follows
Explanation:
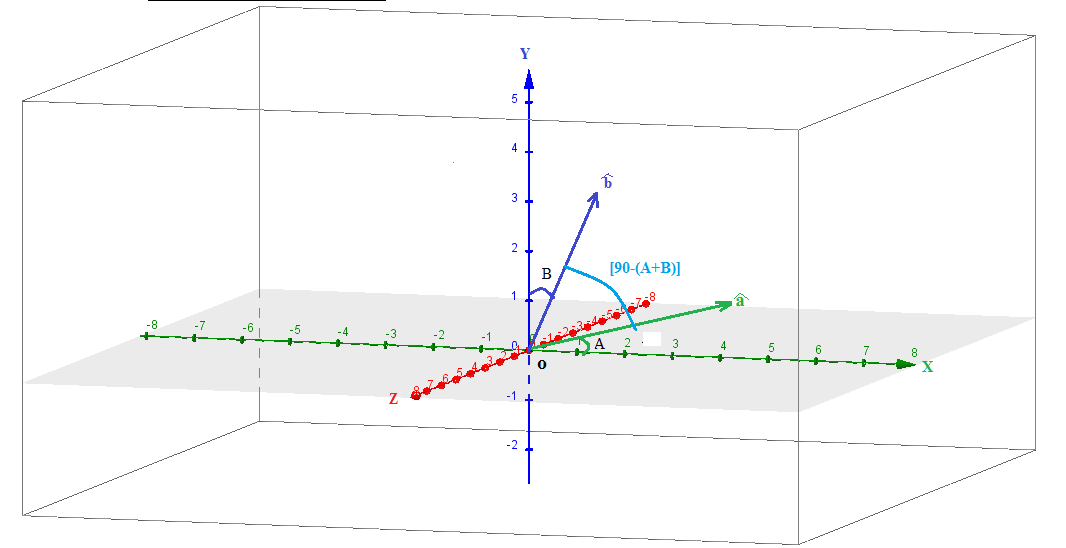
```````````````````````````````````````````````````````````````````````````````````````````````````````````````````
Let us consider two unit vectors in X-Y plane as follows :
#hata-># inclined with positive direction of X-axis at angles A# hat b-># inclined with positive direction of X-axis at angles 90-B, where# 90-B>A# - Angle between these two vectors becomes
#theta=90-B-A=90-(A+B)# ,
Now
Applying Properties of unit vectos
and
Also inserting
Finally we get
```````````````````````````````````````````````````````````````````````````````````````````````````````
Sin(A+B) =SinA CosB + CosASinB formula can also be obtained
by taking scalar product of
Now
Applying Properties of unit vectos
and
Also inserting
Finally we get

