How would you calculate the specific beat of silver, given that 280 g of the metal absorbed 136 calories when changed from 22.13°C to 30.79°C?
1 Answer
Dec 1, 2016
Explanation:
The equation you'll need is the following:
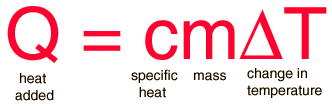
where
Rearrange the equation to isolate

