Question

How would you calculate the surface tension of a 2% (w/v) solution of a wetting agent that has a density of 1.008 g/mL and that rises 6.6 cm in a capillary tube having an inside radius of 0.2 mm?

Answer 1

The surface tension is `"73 mJ·m"^"-2"`.

Explanation:

One method to measure the surface tension of a liquid is to measure the height the liquid rises in a capillary tube.

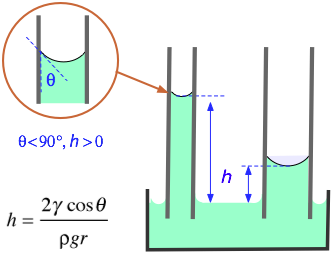
The formula is

`color(blue)(|bar(ul(color(white)(a/a) γ = "rhρg"/"2cosθ" color(white)(a/a)|)))" "`

where

`γ` = the surface tension
`r` = the radius of the capillary
`h` = the height the liquid rises in the capillary
`ρ` = the density of the liquid
`g` = the acceleration due to gravity
`θ` = the angle of contact with the surface

For pure water and clean glass, the contact angle is nearly zero.

If `θ ≈ 0`, then `cosθ ≈ 1`, and the equation reduces to

`color(blue)(|bar(ul(color(white)(a/a) γ = "rhρg"/2 color(white)(a/a)|)))" "`

In your problem,

`r = "0.2 mm" = 2 × 10^"-4"color(white)(l) "m"`
`h = "6.6 cm" = "0.066 m"`
`ρ = "1.008 g/mL" = "1.008 kg/L" = "1008 kg·m"^"-3"`
`g = "9.81 m·s"^"-2"`

`γ = (2 × 10^"-4" color(red)(cancel(color(black)("m"))) × 0.066 color(red)(cancel(color(black)("m"))) × 1008 color(red)(cancel(color(black)("kg·m"^"-3"))) × 9.81 color(red)(cancel(color(black)("m·s"^"-2"))))/2 × ("1 J")/(1 color(red)(cancel(color(black)("kg")))·"m"^2color(red)(cancel(color(black)("s"^"-2"))))= "0.065 J·m"^"-2" = "65 mJ·m"^"-2"`

For comparison, the surface tension of pure water at 20 °C is `"73 mJ·m"^"-2"`.