Question

How would you find the exact value of the six trigonometric function of -45?

Answer 1

`sin(-45^@) = -sqrt(2)/2`

`cos(-45^@) = sqrt(2)/2`

`tan(-45^@) = -1`

`sec(-45^@) = sqrt(2)`

`csc(-45^@) = -sqrt(2)`

`cot(-45^@) = -1`

Explanation:

First let's look at `sin 45^@` and `cos 45^@`

Consider the right angled triangle formed by cutting a `1xx1` square in half diagonally...

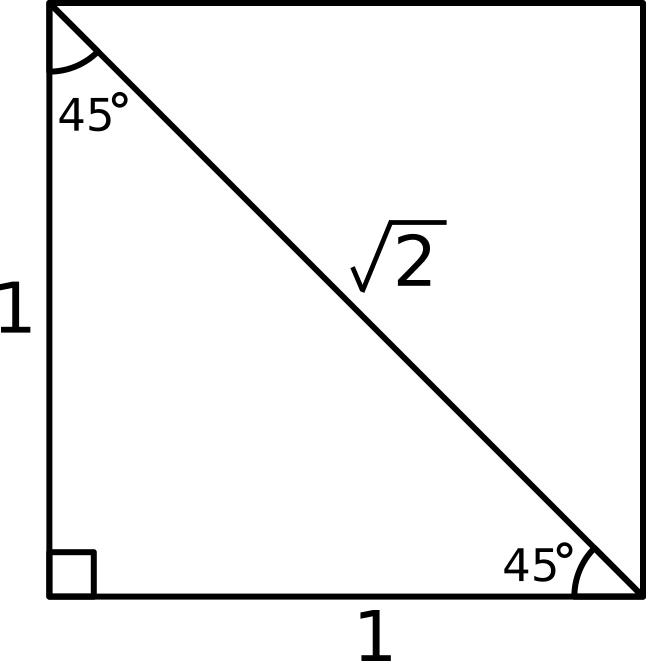
Recall that:

`sin theta = "opposite"/"hypotenuse"`

`cos theta = "adjacent"/"hypotenuse"`

Hence we find:

`sin 45^@ = cos 45^@ = 1/sqrt(2) = sqrt(2)/2`

Next note that `sin` is an odd function and `cos` an even function.

Hence:

`sin(-45^@) = -sin 45^@ = -sqrt(2)/2`

`cos(-45^@) = cos 45^@ = sqrt(2)/2`

Hence we can find the other `4` trigonometric functions:

`tan(-45^@) = sin(-45^@)/cos(-45^@) = (-sqrt(2)/2) / (sqrt(2)/2) = -1`

`sec(-45^@) = 1/cos(-45^@) = 1/(sqrt(2)/2) = 2/sqrt(2) = sqrt(2)`

`csc(-45^@) = 1/sin(-45^@) = 1/(-sqrt(2)/2) = -2/sqrt(2) = -sqrt(2)`

`cot(-45^@) = cos(-45^@)/sin(-45^@) = (sqrt(2)/2)/(-sqrt(2)/2) = -1`