Question

How would you find the exact value of the six trigonometric function of pi/3?

Answer 1

(see below)

Explanation:

Consider an equilateral triangle with sides of length `2`;
each of an equilateral triangle has an angle of `pi/3`

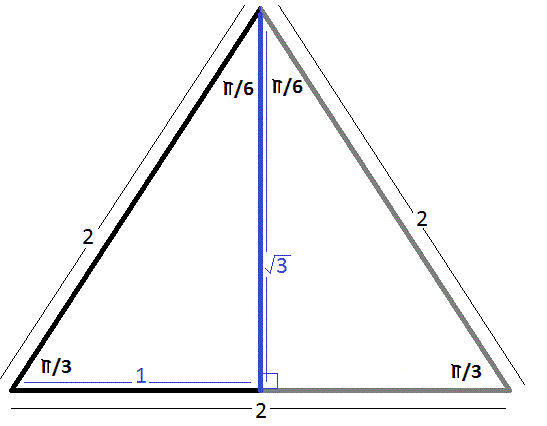
The altitude of the triangle divides the base into two equal length segments; each with a length of `1`.

Using the Pythagorean Theorem, we can find that the height of the triangle is `sqrt(3)`

Considering only one side of the equilateral triangle and the basic trigonometric definitions:

`sin(theta)="opposite"/"hypotenuse" rarr sin(pi/3)=sqrt(3)/2`

`cos(theta)+"adjacent"/"hypotenuse" rarr cos(pi/3)=1/2`

`tan(theta)="opposite"/"adjacent" rarr tan(pi/3)=sqrt(3)`

`csc(theta) ="hypontenuse"/"opposite" rarr csc(pi/3)=2/sqrt(3)=(2sqrt(3))/3`

`sec(theta)="hypotenuse"/"adjacent" rarr sec(pi/3)=2`

`cot(theta)="adjacent"/"opposite" rarr cot(pi/3)1/sqrt(3)=sqrt(3)/3`