Question

How would you show that the polar equation `r=(ed)/(1+ecos(theta))` represents an ellipse if e<1, a parabola if e=1, or a hyperbola if e>1?

`r=(ed)/(1+ecos(theta))`

Answer 1

See below.

Explanation:

We have

`r+e r costheta = e d` but

`{(r cos theta = x),(r = sqrt(x^2+y^2)):}`

then

`sqrt(x^2+y^2) +e x = e d` or

`x^2+y^2 = e^2(x-d)^2` or

`f(x,y) = x^2+y^2 - e^2(x-d)^2=0` or

`f(x,y) = (x,y)((1-e^2,0),(0,1))((x),(y))+((2x)/d-1)d^2e^2=0`

The conic characterization is done according do the eigenvalues of

`((1-e^2,0),(0,1))` which are `{1-e^2,1}`

thus

`{(e < 1-> "ellipse - (both positive)" ),(e = 1 -> "parabola - (one null)"),(e > 1-> "hyperbola - (one positive other negative)"):}`

Answer 2

Please see below.

Explanation:

We know that a conic section is defined as locus of a point that moves so that ratio, known as `e`, of its distance from a fixed point called focus and a given line called directrix is always constant.

1. in case this ratio is equal to one, it is a parabola,

2. in case this ratio is less than one, it is an ellipse and

3. in case this ratio is greater than one, it is a hyperbola.

Assume that in polar coordinates, focus is at pole and directrix is at a distance of `d` to the left of pole and perpendicular to polar axis.

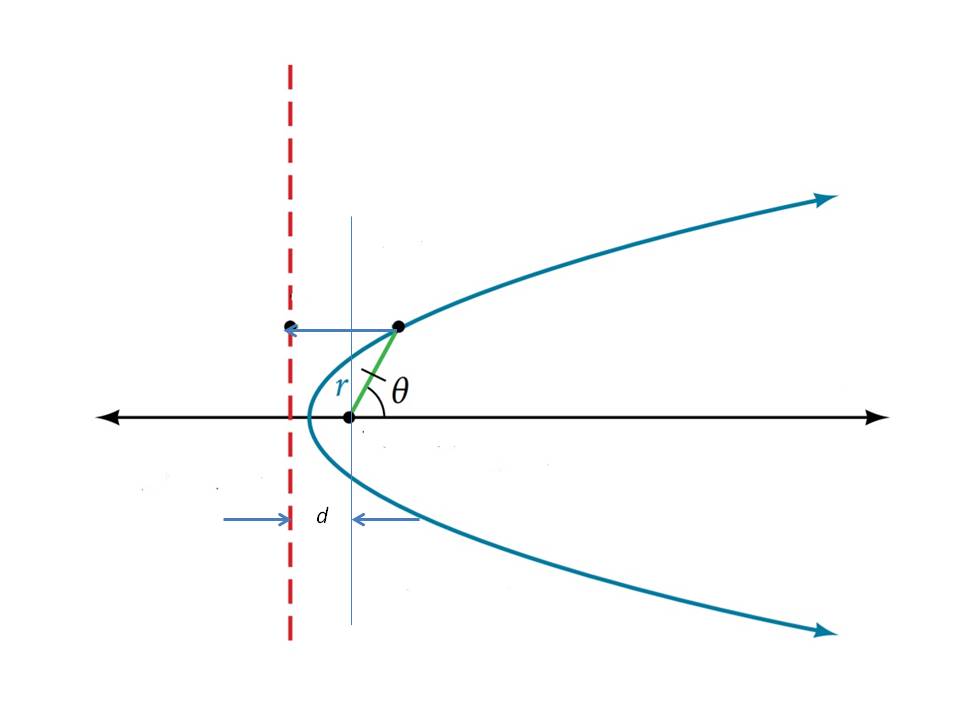
Now if `(r,theta)` is a point on the conic section, then its distance from focus is of course `r`. For distance between the point and directrix, we can split it in two parts, of which one is `d` and ther is `rcostheta`. Hence this distance is `d+rcostheta`

and equation of conic section is

`r/(d+rcostheta)=e`

or `r=ed+ercostheta`

or `r(1-ecostheta)=ed`

and `r=(ed)/(1-ecostheta)`

Observe that if directrix is to the right of focus, the equation of conic section would have been `r=(ed)/(1+ecostheta)`