Question

How would you use the mass spectrum of rubidium to determine the atomic mass of rubidium?

Answer 1

See graph below.
`85*(1-.38)+87*0.38 = 85.76 am u`

Not too far off the actual! (85.4678)

Explanation:

A mass spectrum is an output from a mass spectrometer.

Mass spectrometers are used for finding relative abundances of selected isotopes by ionizing a sample, accelerating the sample, then as a function of the ions' mass/charge, each bends around the corner, interacting with the magnet in characteristic bends, which travel to the detector, see below:

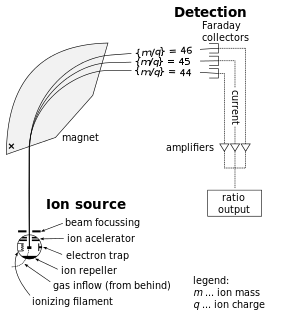
Then, the detector generates a graph of atomic weight versus detector signal (e.g. abundance).

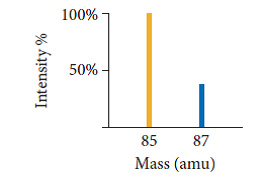
This question is asking us to interpret the graph. This is Rubidium (maybe even the one you're looking at).

The atomic mass is a sum function of relative abundances of isotopes.

`sum = A*M`

Where,

M = isotopic mass
A = relative abundance

`85*(1-.38)+87*0.38 = 85.76 am u`

Not too far the actual! (85.4678)