Question

How would you write a full set of quantum numbers for the first, third, and fourteenth electron removed from the the ground state of a Cu atom?

Answer 1

Here's what I got.

Explanation:

Your starting point here is the electron configuration for a ground state copper atom, which looks like this - I won't use the noble gas shorthand notation for this one

`"Cu: " 1s^2 2s^2 2p^6 3s^2 3p^ 3d^10 4s^1`

Now, electrons are removed from any atom in order of decreasing energy level. Simply put, the electrons are removed from the orbitals that are highest in energy first.

As you know, you have a total of four quantum numbers used to describe the exact location of an electron that surrounds the nucleus, and the spin of said electron.

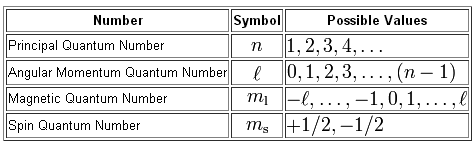
So, let's identify the first electron that will be removed from a ground state copper atom and write out its quantum number set.

As you can see, the 4s-orbital is highest in energy, since it's located on the fourth energy level. This means that the electron that occupies this orbital will have

• `n=4 ->` located on the fourth energy level
• `l =0 ->` located in the s-subshell
• `m_l = 0 ->` located in an s-orbital
• `m_s = +1/2 ->` it has spin-up

Removing this electron will lead to the formation of the `"Cu"^(+)` cation, which has the following electron configuration

`"Cu"^(+): 1s^2 2s^2 3p^6 3s^2 3p^6 3d^10`

Now, the third electron that is removed from the neutral copper atom is equivalent to the second electron removed from the `"Cu"^(+)` cation.

The orbitals highest in energy are now the 3d-orbitals. An important thing to remember is that you will remove electrons from completely filled 3d-orbitals first, then move on to half-filled 3d-orbitals.

So, the quantum number set that describes this electron will be

• `n=3 ->` located on the third energy level
• `l=2 ->` located in the d-subshell
• `m_l = -1 ->` located in the `3d_(xy)` orbital
• `m_s = -1/2 ->` has spin-down, since it's assumed that the first electron placed in an empty orbital has `m_s = +1/2`

Now to remove the fourteenth electron from a neutral copper atom. As you can see, in a neutral copper atom, the 3d-subshell contains a total of `10` electrons, `2` per orbital.

This means that removing the first `11` electrons from the neutral copper atom will leve you with

`"Cu"^(11+): 1s^2 2s^2 2p^6 3s^2 3p^6`

Notice that removing `2` electrons more will leave you with

`"Cu"^(13+): 1s^2 2s^2 2p^6 3s^2 3p^4`

Finally, you can say for sure that the fourteenth electron will be removed from a 3p-orbital that is completely filled, since the last two electrons came from completely filled 2p-orbitals as well.

You can thus say that the quantum number set for this electron will be

• `n=3 ->` once again, located on the third energy level
• `l=1 ->` located in the p-subshell
• `m_l = 1 ->` located in the `2p_z` orbital
• `m_s = -1/2 ->` has spin-down since it's the first electron to be removed from that respective orbital