How would you write a full set of quantum numbers for the outermost electron in an Rb atom?
1 Answer
Explanation:
Start by writing the complete electron configuration fir a neutral rubidium atom.
Rubidium,
#"Rb: " 1s^2 2s^2 2p^6 3s^2 3p^6 3d^10 4s^2 4p^6 color(red)(5)s^1#
So, the outermost electron in a rubidium atom is located on the fifth energy level, in an s-orbital.
As you know, four quantum numbers are used to describe the position and spin of an electron inside an atom.
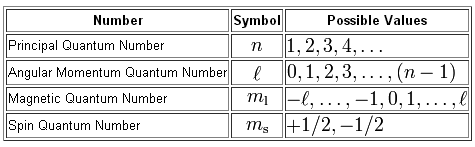
The principal quantum number,
The angular momentum quantum number,
#l=0 -># s-subshell#l=1 -># p-subshell#l=2 -># d-subshell
and so on. Since your electron is located in the s-subshell, you will have
The magnetic quantum number,
Finally, the spin quantum number,
#m_s = +1/2 -># spin-up electron#m_s = -1/2 -># spin-down electron
For you electron, you can select
#n=5, l=0, m_l =0, m_s = +1/2#
The electron is located on the fifth energy level, in the 5s-subshell, in the 5s-orbital, and has spin-up.

