Question

Find `j(x)`. What type of wave this is describing?

Answer 1

`j(x)` is NOT a wave function! It does not describe a wave at all. In fact, we could choose any arbitrary wave, and it would not change the definition of `j(x)`.

The probability current, `j(x,t)`, is the flow of probability through a certain unit area per unit time. We could then predict that `j(x)` is a constant w.r.t. position, as the probability density does not vary if we only look at some initial state `j(x,0)`.

---

`(i)`

Well, if we want to show that `j(x)` is a constant w.r.t. `x`, we just need

`(dj(x))/(dx) = 0`.

So... we first find the form of `(dj(x))/(dx)`.

`(dj(x))/(dx) = d/(dx)[(iℏ)/(2m)(psi (dpsi^"*")/(dx) - psi^"*" (dpsi)/(dx))]`

`= (iℏ)/(2m)(psi (d^2psi^"*")/(dx^2) + cancel((dpsi)/(dx) (dpsi^"*")/(dx)) - psi^"*" (d^2psi)/(dx^2) - cancel((dpsi^"*")/(dx)(dpsi)/(dx)))`

The time-independent Schrodinger equation is

`-ℏ^2/(2m) (d^2psi)/(dx^2) + V(x)psi = Epsi`

so we have:

`(d^2psi)/(dx^2) = -(2m(E-V(x)))/(ℏ^2)psi`

`(d^2psi^"*")/(dx^2) = -(2m(E-V(x)))/(ℏ^2)psi^"*"`

Therefore:

`(dj(x))/(dx) = (iℏ)/(2m)(psi [-(2m(E-V(x)))/(ℏ^2)psi^"*"] - psi^"*" [-(2m(E-V(x)))/(ℏ^2)psi])`

`= -(iℏ)/(2m)((2m(E-V(x)))/(ℏ^2)psipsi^"*" - (2m(E-V(x)))/(ℏ^2)psi^"*"psi)`

Obviously, `psi` commutes with `psi^"*"`, so

`color(blue)((dj(x))/(dx)) = -(iℏ)/(2m) cdot (2m(E-V(x)))/(ℏ^2) cdot (psi^"*"psi - psi^"*"psi)`

`= color(blue)(0)`

Thus, `j(x)` is a constant w.r.t. `x`.

`(ii)`

We consider the plane wave `psi(x) = Ae^(ikx) + Be^(-ikx)`, with `k` being the usual wave number `k = p/ℏ`.

It has some probability of reflection or transmission (we do not know what, until we know the properties of `V` as a function of `x`), and its derivatives are:

`(dpsi)/(dx) = ikAe^(ikx) - ikBe^(-ikx)`

`(dpsi^"*")/(dx) = -ikA^"*"e^(-ikx) + ikB^"*"e^(ikx)`

Therefore, for this `psi(x)`:

`color(blue)(j_1(x)) = (iℏ)/(2m)[(Ae^(ikx) + Be^(-ikx))(-ikA^"*"e^(-ikx) + ikB^"*"e^(ikx)) - (A^"*"e^(-ikx) + B^"*"e^(ikx))(ikAe^(ikx) - ikBe^(-ikx))]`

`= (iℏ)/(2m)[-ikA A^"*" + cancel(ikAB^"*"e^(2ikx)) - cancel(ikBA^"*"e^(-2ikx)) + ikBB^"*" - ikA A^"*" + cancel(ikBA^"*"e^(-2ikx)) - cancel(ikAB^"*"e^(2ikx)) + ikBB^"*"]`

`= (iℏ)/(cancel(2)m)[cancel(2)ik(B B^"*" - A A^"*")]`

`= color(blue)((ℏk)/m(A A^"*" - B B^"*"))`

For `psi(x) = Fe^(ikx)`,

`(dpsi)/(dx) = ikFe^(ikx)`

`(dpsi^"*")/(dx) = -ikF^"*"e^(-ikx)`

Thus:

`color(blue)(j_2(x)) = (iℏ)/(2m)[Fcancel(e^(ikx))(-ikF^"*"cancel(e^(-ikx))) - F^"*"cancel(e^(-ikx))(ikFcancel(e^(ikx)))]`

`= (iℏ)/(2m)[-ikF F^"*" - ikF F^"*"]`

`= (iℏ)/(cancel(2)m)[-cancel(2)ikF F^"*"]`

`= color(blue)((ℏk)/(m)F F^"*")`

The terms `A A^"*"`, etc. indicate the probability of the event occurring corresponding to its `e^(pmikx)` term. Of course, this means that

• the first plane wave has some finite probability of moving forward (`e^(ikx)`) or moving backward (`e^(-ikx)`).
• the second plane wave obviously has a `100%` probability of moving forward (`e^(ikx`) (how else would it move?).

`(iii)`

This is a pretty roundabout way of simply saying to place a barrier of arbitrary height in front of the particle of width `2a` centered at `x = 0`:

`V(x) = {(0, |x| > a),(V_0, -a <= x <= a):}`

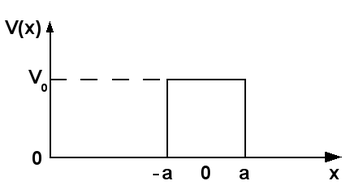
Here we define `k` on the left of the barrier and `k'` on the right of the barrier (`k ne k'`). That is, we define the wave functions for the left and right of the barrier as:

`psi_L(x) = Ae^(ikx) + Be^(-ikx)`

`psi_R(x) = Fe^(ik'x)`

where `psi_R(x)` necessarily has no `Ge^(-ik'x)` term so that the particle does not double back.

Therefore, what we got in `(ii)` is now specified:

`j_L(x) = (ℏk)/m(A A^"*" - B B^"*") = "const"`

`j_R(x) = (ℏk')/mFF^"*" = "const"`

From `(i)`, since `j(x)` is a constant w.r.t. `x` (which we see here) `j_L(x) = j_R(x) = "same const"`.

The reflection coefficient is defined as

`R = (B B^"*")/(A A^"*")`

And the transmission coefficient is defined as

`T = (k')/(k)(F F^"*")/(A A^"*")`

First, we can say that

`overbrace(cancel((ℏ)/m)k(A A^"*" - B B^"*"))^(j_L(x)) = overbrace(cancel((ℏ)/m)k'FF^"*")^(j_R(x))`

or that

`-(A A^"*" - B B^"*") = B B^"*" - A A^"*" = -(k')/k FF^"*"`

Therefore, we use our results to find:

`color(blue)(R + T) = (B B^"*")/(A A^"*") + (k')/(k)(F F^"*")/(A A^"*")`

`= (B B^"*" + A A^"*" - A A^"*")/(A A^"*") + (k')/(k)(F F^"*")/(A A^"*")`

`= 1 + (B B^"*" - A A^"*")/(A A^"*") + (k')/(k)(F F^"*")/(A A^"*")`

`= 1 - cancel((k')/k (FF^"*")/(A A^"*") + (k')/(k)(F F^"*")/(A A^"*"))`

`= color(blue)(1)`

This result should make sense.

Obviously, a particle can only reflect or transmit through a potential barrier. There is nothing else it can physically do, so this total probability should be `100%`.