Question

I am unsure of a few steps. Can someone help me?:)

Solve each system by the graphing method.

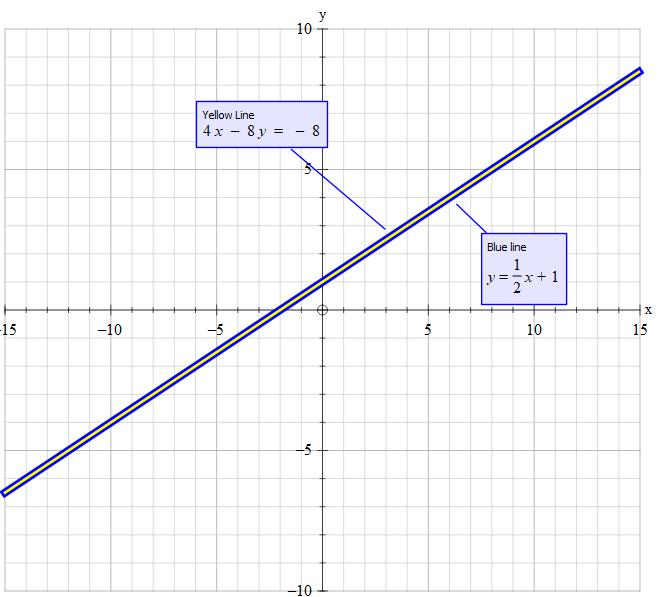
y = 1/2x + 1
4x - 8y = -8

a. Infinite solutions
b. (1, -8)
c. (1, 4)
d. No solution

Answer 1

a.) Infinite Solutions

Explanation:

graph{y=0.5x+1 [-10, 10, -5, 5]}
By graphing both on a plot, we can see that they are the same line. Therefore, there are infinite solutions to this.

If you wanted to do it analytically, you could solve the second equation for y:

`4x-8y= -8` Subtract `4x` over
`-8y=-8color(red)(-4x)` Divide both sides by `-8`
`y=(-8-4x)/color(red)(-8)` Simplify
`y=1+x/2`

This equation is equal to the first equation, so there will be infinite solutions.

Hope this helped!

Answer 2

Very detailed explanation given in the beginning using first principles to demonstrate where the shortcut methods come from.

Explanation:

Given:

`y=1/2x+1" "..........Equation(1)`
`4x-8y=-8" ".....Equation(2)`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

It is much easier to graph a straight line equation if it is in the form
`y=mx+ c` where `m` is the slope (gradient) and `c` is some constant value

Lets manipulate `Eqn(2)` into this format

`color(blue)("Step 1 - Get the "y" term on its own")`

We need to 'get rid of the `4x` on the left. We do this by turning it into 0 as anything + 0 does not change.

subtract `color(red)(4x)` from `ul("both sides.")`

`color(green)(4x-8ycolor(white)("d") =color(white)("d") -8color(white)("ddd")->color(white)("ddd")ubrace(4xcolor(red)(-4x))-8ycolor(white)("d")=color(white)("d")-8color(red)(-4x))`

`color(green)(color(white)("ddddddddddddddddd")->color(white)("dddd.d")0color(white)("dd")-8ycolor(white)("d")=-4x-8)`

`color(blue)("Step 2 - Get the "y" on its own")`

We need to get rid of the `8` in `-8y` so turn it into 1 as `1xxy=y`

Divide all of `ul("both sides")` by `color(red)(8)`

`color(green)(-8ycolor(white)("d")=color(white)("d")-4x-8 color(white)("ddd")->color(white)("ddd")-8/color(red)(8) y=-4/color(red)(8)x-8/color(red)(8) )`

`color(green)(color(white)("ddddddddddddddddddd")->color(white)("dddd")-y=-1/2x-1 )`

`color(blue)("Step - Make the "y" positive")`
Make `y` positive by multiplying everything `ul("on both sides")` by `(-1)` giving:

`y=1/2x+1" ".....................Equation(2_a)`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(magenta)("Spot anything?")`

Notice that `Eqn(1) and Eqn(2_a)` are the same.

This means that `Eqn(2_a)` sits on top of `Eqn(1)`

So there is an infinite count of shared points