Ibuprofen has the following mass percent composition. What is the empirical formula of ibuprofen?

2 Answers
The empirical formula is
Explanation:
With all these sorts of problems, we assume a mass of
We divide thru by the LOWEST molar quantity (that of oxygen) to get a trial empirical formula of
For completeness, we could quote a molecular formula IF WE HAD a molecular mass determination for Ibuprofen.......but we do, it is
Now the MOLECULAR formula is always a multiple of the empirical formula, i.e:
Clearly,
The empirical formula for ibuprofen is
Explanation:
The empirical formula of a compound represents the lowest whole number ratio of the elements in it. Because the percentages of carbon, hydrogen, and oxygen add up to 100%, you can directly convert them into grams.
The moles of each element must be determined. Then the mole ratio of each element is calculated by dividing by the smallest number of moles. To calculate the empirical formula, you may need to manipulate the mole ratios, such as multiplying by two.
Determine the Moles of Each Element
Divide the given mass by the molar mass of each element. The molar mass of an element is the atomic weight (relative atomic mass) on the periodic table in grams/mole, or g/mol.
Determine the Mole Ratio for Each Element.
Divide the moles of each element by the smallest number of moles.
Empirical Formula
Since
The empirical formula for ibuprofen is
It is also its molecular formula.
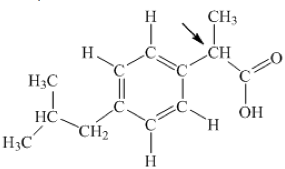
The diagram below represents the structural formula for ibuprofen.