If 1 mmole of NaOH is added into a solution in which there is 8 mmoles of aspartic acid with a net -1 charge and 10 moles of aspartic acid with a ned -2 charge, what would the pH of the solution be?
1 Answer
Explanation:
! LONG ANSWER !!
The idea here is that aspartic acid,
For simplicity, I'll use
These pH values will depend on the acid's
#{(pK_(a1) = 1.99), (pK_(a2) = 3.90), (pK_(a3) = 9.90) :}#
http://academics.keene.edu/rblatchly/Chem220/hand/npaa/aawpka.htm
Here's how a molecule of aspartic acid looks like when fully protonated
This is the form you get at pH values that are below
Here's how a titration would look like for the titration of aspartic acid with a strong base
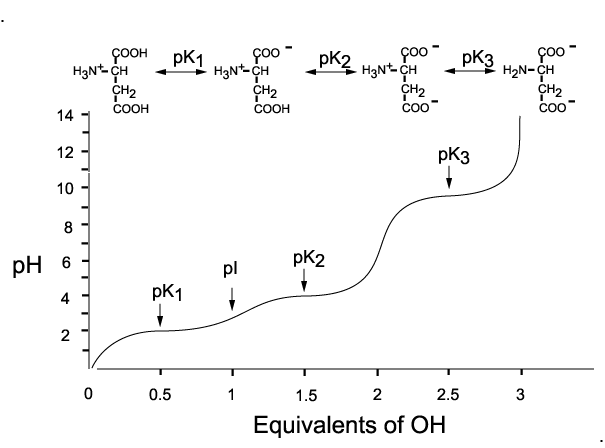
As the pH of the solution increases from
At this point, the molecule is neutral, since the
The same thing happens as the pH increases from
At this point, the molecule carries a
Finally, at pH values that exceed
At this point, the molecule carries a
So, you know that your solution contains the
Since
This means that you can use the Henderson - Hasselbalch equation to help you figure out the pH of the solution
#color(blue)("pH" = pK_a + log( (["conjugate base"])/(["weak acid"])))#
Since
Right from the start, you can tell that the pH of the solution before adding the base is higher than
Now, sodium hydroxide is a strong base that dissociates in a
The hydroxide anions will then neutralize the
#"HA"_text((aq])^(-) + "OH"_text((aq])^(-) -> "A"_text((aq])^(2-) + "H"_2"O"_text((l])#
You have
This means that
After the reaction is complete, the solution will contain
#n_(OH^(-)) = "0 moles" -># completely consumed by the reaction
#n_("HA"^(-)) = "8 mmoles" - "1 mmole" = "7 mmoles"#
#n_(A^(2-)) = "10 mmoles" + "1 mmole" = "11 mmoles"#
This means that you have
#"pH" = pK_(a3) + log( (["A"^(2-)])/(["HA"^(-)]))#
Since the volume of the buffer is the same for all species, you can use the number of moles in the H - H equation.
Therefore,
#"pH" = 9.90 + log( (11 color(red)(cancel(color(black)("mmoles"))))/(7color(red)(cancel(color(black)("mmoles"))))) = color(green)(10.1)#

