If #A = <3 ,-1 ,5 >#, #B = <5 ,2 ,-9 ># and #C=A-B#, what is the angle between A and C?
1 Answer
Explanation:
The angle
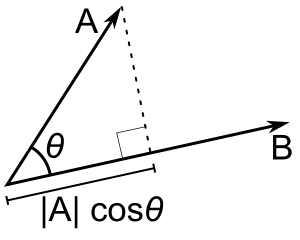
# vec A * vec B = ||A|| \ ||B|| \ cos theta #
By convention when we refer to the angle between vectors we choose the acute angle.
So for this problem,
#vec A=<<3,-1,5>>#
#vec B=<<5,2,-9>>#
And so;
# vec C = vec A - vec B #
# \ \ \ \ = <<3,-1,5>> - <<5,2,-9>> #
# \ \ \ \ = <<-2,-3,14>> #
The moduli are given by;
# || vec A || = || <<3,-1,5>> || #
# \ \ \ \ \ \ \ \ = sqrt( (3)^2+(-1)^2+(5)^2 ) #
# \ \ \ \ \ \ \ \ = sqrt( 9 + 1 + 25 ) #
# \ \ \ \ \ \ \ \ = sqrt( 35 ) #
# || vec C || = || <<-2,-3,14>> || #
# \ \ \ \ \ \ \ \ = sqrt( (-2)^2+(-3)^2+(14)^2 ) #
# \ \ \ \ \ \ \ \ = sqrt( 4 + 9 + 196 ) #
# \ \ \ \ \ \ \ \ = sqrt( 209 ) #
And the scaler product is:
# vec A * vec C = || <<3,-1,5>> || * || <<-2,-3,14>> || #
# \ \ \ \ \ \ \ \ \ \ = (3)(-2) + (-1)(-3) + (5)(14)#
# \ \ \ \ \ \ \ \ \ \ = -6 + 3 + 70#
# \ \ \ \ \ \ \ \ \ \ = 67#
And so using
# 67 = sqrt(35) * sqrt(209) * cos theta #
# :. cos theta = (67)/(sqrt(7315))#
# :. cos theta = 0.783371 ... #
# :. theta = 38.43 °# (2dp)
So the acute angle between the vectors is

