Angle between Vectors

Key Questions

  • What are common mistakes students make with angles between vectors?

    When we are to consider the angle between any two vectors, it should be noted that the angle which is less than #pi# is to be taken.

    Aritra G. · 1 · May 30 2015
  • How do I calculate the angle between two vectors?

    You can use the dot product to solve this problem. See http://en.wikipedia.org/wiki/Dot_product

    The dot product is an operation on two vectors. There are two different definitions of dot product. Let #\vec(A)=[A_1,A_2,...,A_n]# be a vector and #\vec(B)=[B_1,B_2,...,B_n]# be another vector, then we have 2 formulas for dot product:

    1) Algebraic definition:

    #\vec(A) \cdot \vec(B) = \sum_1^n A_i B_i = A_1 B_1 + A_2 B_2 + ... + A_n B_n#

    2) Geometric definition:

    #\vec(A) \cdot \vec(B) = ||\vec(A)||\ ||\vec(B)||\cos(\theta)#

    where #\theta# is the angle between #\vec(A)# and #\vec(B)#, and #||\vec(A)||# denotes the magnitude of #\vec(A)# and has the formula:

    #||\vec(A)|| = \sqrt(A_1^2 + A_2^2 + ... + A_n^2)#

    We can solve many questions (such as the angle between two vectors) by combining the two definitions:

    #\sum_1^n A_i B_i = ||\vec(A)||\ ||\vec(B)||\cos(\theta)#

    or

    #A_1 B_1 + A_2 B_2 + ... + A_n B_n = (\sqrt(A_1^2 + A_2^2 + ... + A_n^2))(\sqrt(B_1^2 + B_2^2 + ... + B_n^2))\cos(\theta)#

    If we have two vectors, then the only unknown is #\theta# in the above equation, and thus we can solve for #\theta#, which is the angle between the two vectors.

    Example:

    Q: Given #\vec(A) = [2, 5, 1]#, #\vec(B) = [9, -3, 6]#, find the angle between them.

    A:
    From the question, we see that each vector has three dimensions. From above, our formula becomes:

    #A_1 B_1 + A_2 B_2 + A_3 B_3 = (\sqrt(A_1^2 + A_2^2 + A_3^2))(\sqrt(B_1^2 + B_2^2 + B_3^2))\cos(\theta)#

    Left side:

    #A_1 B_1 + A_2 B_2 + A_3 B_3 = (2)(9) + (5)(-3) + (1)(6) = 9#

    Right side:

    #||\vec(A)|| = \sqrt(A_1^2 + A_2^2 + A_3^2) = \sqrt(2^2 + 5^2 + 1^2) = \sqrt(30)#
    #||\vec(B)|| = \sqrt(B_1^2 + B_2^2 + B_3^2) = \sqrt(9^2 + (-3)^2 + 6^2) = \sqrt(126)#
    #\theta# is unknown

    Plug everything into the formula, we get:

    #9 = (\sqrt(30))(\sqrt(126))\cos(\theta)#

    Solve for #\theta#:

    #\cos(\theta) = \frac(9)((\sqrt(30))(\sqrt(126))#
    #\theta = \cos^-1(\frac(9)((\sqrt(30))(\sqrt(126))))#

    Using a calculator, we get:

    #\theta = 81.58# degrees

    See the following video of ...

    Angle Between Vectors Example

    R · · Aug 29 2014
  • What is the dot product of two vectors that are parallel?

    It is simply the product of the modules of the two vectors (with positive or negative sign depending upon the relative orientation of the vectors).
    A typical example of this situation is when you evaluate the WORK done by a force #vecF# during a displacement #vecs#.
    For example, if you have:
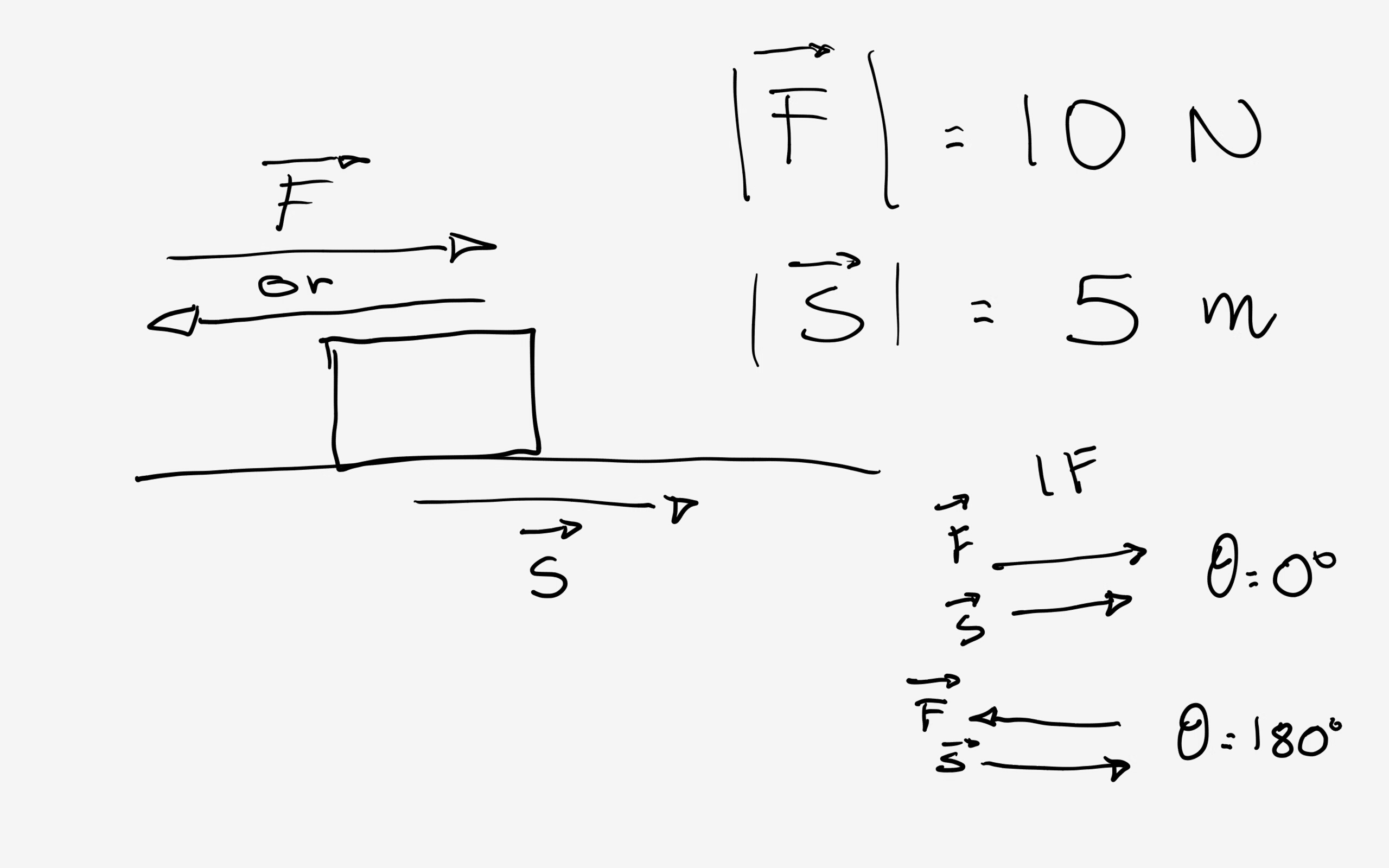
    enter image source here
    Work done by force #vecF#:
    #W=|vecF|*|vecs|*cos(theta)#
    Where #theta# is the angle between force and displacement; the two vectors being parallel can give:

    #theta=0°# and #cos(theta)=cos(0°)=1# so:
    #W=5*10*1=50 J#

    Or:

    #theta=180°# and #cos(theta)=cos(180°)=-1# so:
    #W=5*10*-1=-50 J#

    Gió · 1 · Jan 15 2015
  • What is the dot product of two vectors that are perpendicular?

    The dot of two vectors is given by the sum of its correspondent coordinates multiplied. In mathematical notation:
    let #v = [v_(1), v_(2), ... , v_(n)] # and #u = [u_(1), u_(2), ... , u_(n)]#,
    Dot product:
    #v*u = #
    #sum v_(i).u_(i) = (v_(1).u_(1)) + (v_(2).u_(2)) + ... + (v_(n).u_(n))#

    and angle between vectors:
    #cos(theta) =(v*u)/(|v||u|)#

    Since the angle between two perpendicular vectors is #pi/2#, and it's cosine equals 0:
    #(v*u)/(|v||u|) = 0 :. v*u = 0#

    Hope it helps.

    Bernardo Russo G. Ferreira · · Oct 2 2014

Questions

Dot Product of Vectors