If a histogram is unimodal and symmetric, what well-known curve will the histogram approximate?
1 Answer
This question is likely pointing towards a normal curve.
However, there is much more to the answer and this is not always the case. While the normal curve is the most common unimodal, symmetric distribution, there are many other distributions that are unimodal and symmetric.
Let's start by thinking about what this set of distributions will look like. First, the mode MUST be in the center of the distribution. Because the distribution is symmetric, if there were a mode that was anywhere but the center, then there would be at least 2 modes (one on each side of center).
Second, we know that all distributions have a total area under the curve of 1. This means that the area under the curve of each side is equal to 0.5.
What this leaves us with is any distribution where there is no decrease on the left side, reaches the center, and then does the exact same in reverse on the other side, as long as the area of the curve is 0.5 on each side. The normal curve certainly fits this description, but so do many other named distributions, such as the t-distribution, and many other distributions that you can create for yourself.
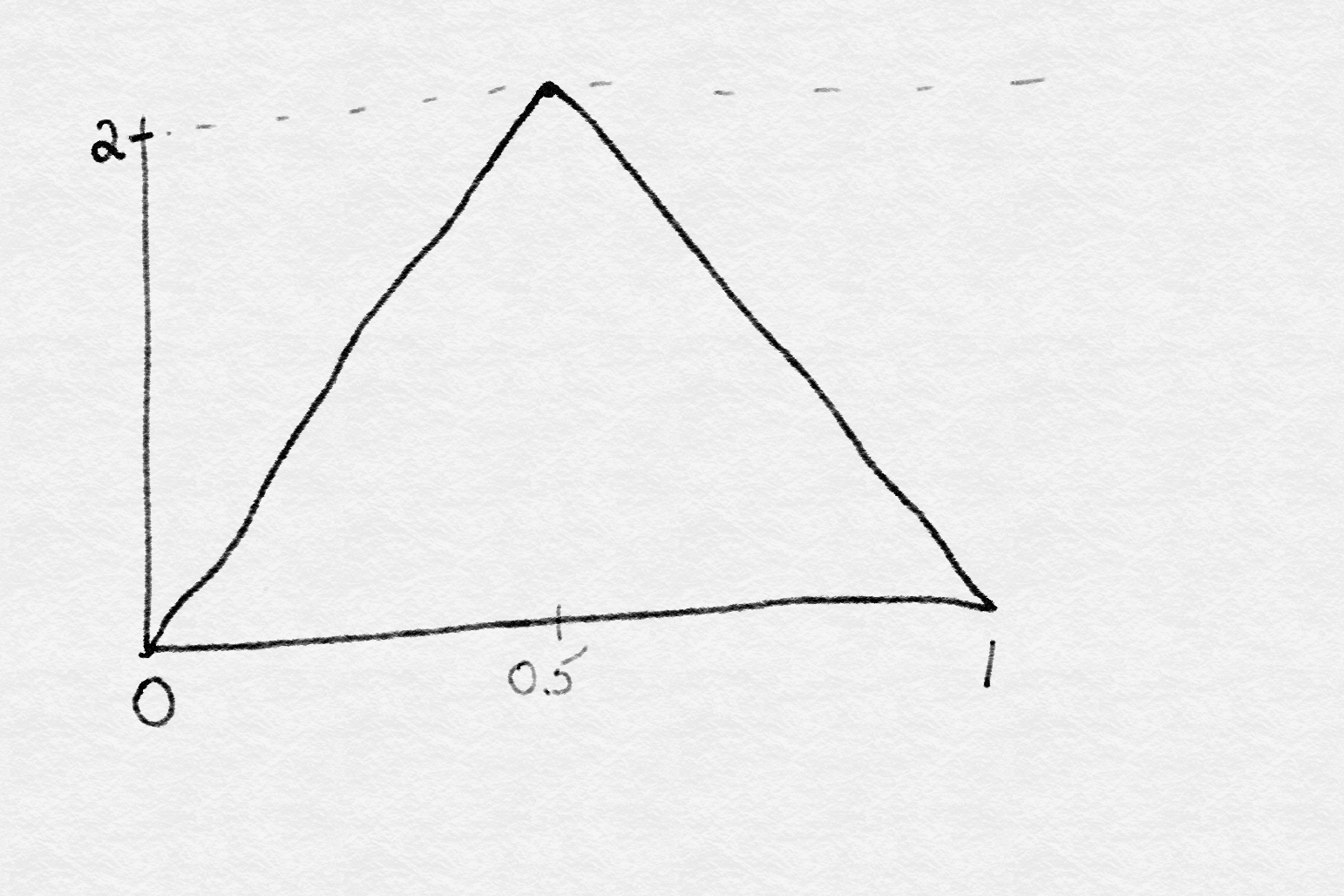
One example of this is what I will call a triangle distribution. See that the distribution below fits all of the criteria of the question, but is very different from a normal curve: