If a sample of gas occupies 6.80 L at 325°C, what will be its volume at 25°C if the pressure does not change?
1 Answer
Explanation:
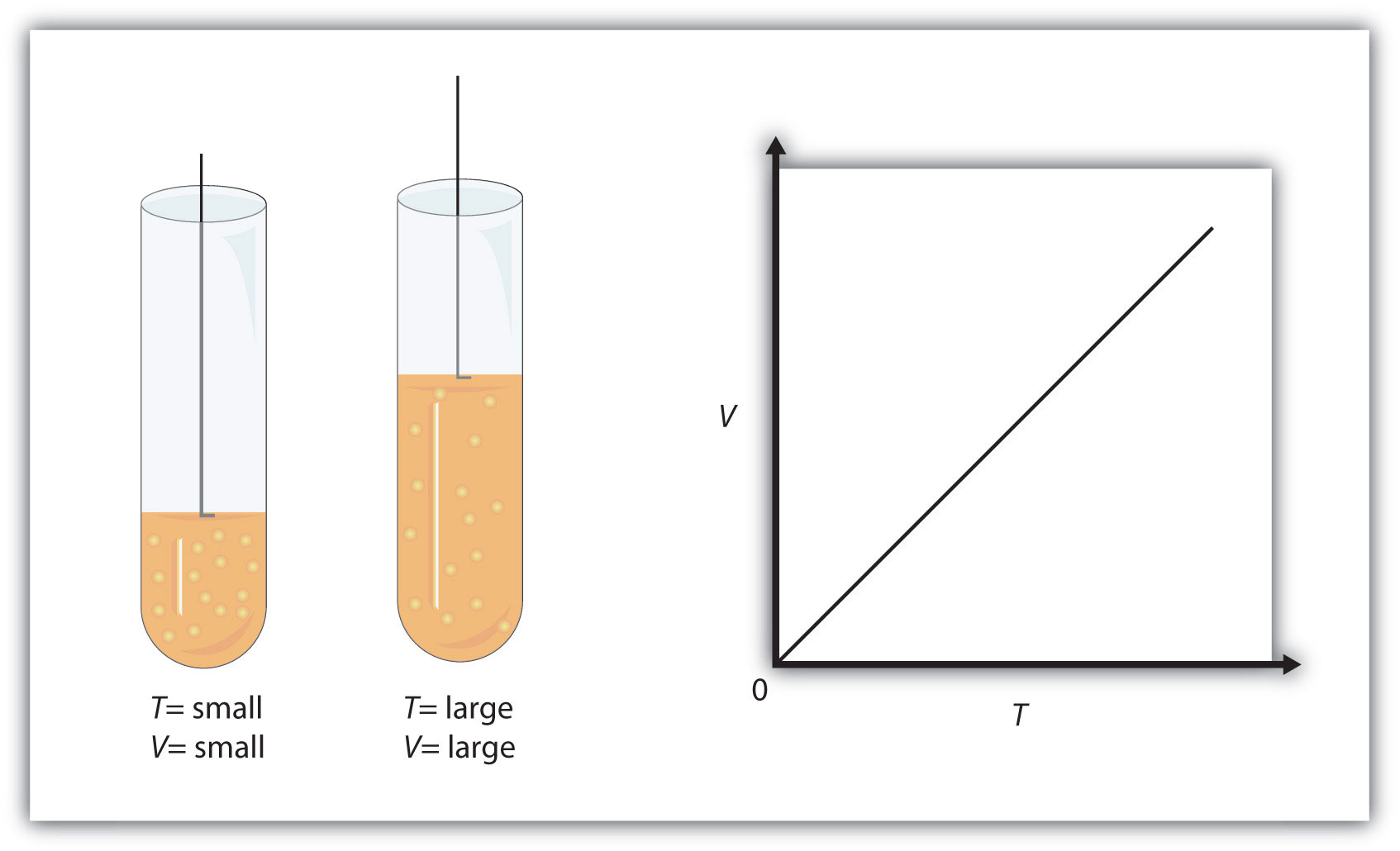
Even without doing any calculations, you should be able to look at the values given to you and predict that the volume of the gas will decrease as temperature decreases.
When pressure and number of moles of gas are held constant, the volume of a gas and its temperature have a direct relationship - this is known as Charles' Law.
As you know, gas pressure is caused by the collisions that take place between the molecules of gas and the walls of the container.
The more powerful and frequent these collisions are, the higher the pressure of the gas.
Now, temperature is a measure of the average kinetic energy of the gas molecules. When you decrease temperature, you're essentially decreasing the average speed with which these molecules hit the walls of the container.
Because molecules are hitting the walls of the container with less force, you need these collisions to be more frequent in order for pressure to be constant.
This means that the volume of the gas must decrease as well, since the same number of molecules in a smaller volume will result in more frequent collisions with the walls of the container.
So, when temperature decreases, volume decreases as well.
Mathematically, this is written as
#color(blue)(|bar(ul(color(white)(a/a)V_1/T_1 = V_2/T_2color(white)(a/a)|)))" "# , where
Now, it's very important to remember that you must use absolute temperature, i.e. the temperature expressed in Kelvin.
To go from degrees Celsius to Kelvin, use the conversion factor
#color(blue)(|bar(ul(color(white)(a/a)T["K"] = t[""^@"C"] + 273.15color(white)(a/a)|)))#
So, rearrange the equation for Charles' Law and solve for
#V_1/T_1 = V_2/T_2 implies V_2 = T_2/T_1 * V_1#
Plug in your values to get
#V_2 = ((273.15 + 25)color(red)(cancel(color(black)("K"))))/((273.15 + 325)color(red)(cancel(color(black)("K")))) * "6.80 L" = "3.3895 L"#
You need to round this off to two sig figs, the number of sig figs you have for the final temperature of the gas
#V_2 = color(green)(|bar(ul(color(white)(a/a)"3.4 L"color(white)(a/a)|)))#

