Question

If `f(x)=x^(1/2)`, `1 <= x <= 4` approximate the area under the curve using ten approximating rectangles of equal widths and left endpoints?

Answer 1

Area `~~ 4.5148` (4dp)

Explanation:

We have:

`f(x) = sqrt(x)`

We want to calculate over the interval `[1,4]` with `10` strips; thus:

`Deltax = (4-1)/10 = 0.3`

Note that we have a fixed interval (strictly speaking a Riemann sum can have a varying sized partition width). The values of the function are tabulated as follows;

Left Riemann Sum

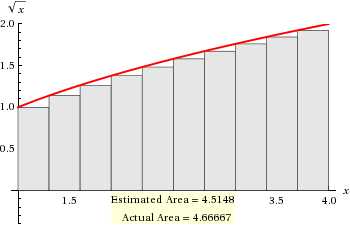
`LRS = sum_("left") f(x)Deltax`
`" " = (0.3) { f(1)+f(1.3) + f(1.6) + ... +f(3.4) + f(3.7) } \ \ \` (The LHS values)

`" " = 0.3*(1+1.140175425+1.264911064+1.378404875+`
`" " 1.483239697+1.58113883+1.673320053+`
`" " 1.760681686+1.843908891+1.923538406`

`" " = 0.3*15.04931893`
`" " = 4.514795679`

Actual Value

For comparison of accuracy:

`Area = int_1^4 \ x^(1/2) \ dx`
`" " = [(x^(3/2))/(3/2)]_1^4`
`" " = 2/3[x^(3/2)]_1^4`
`" " = 2/3{(8) - (1)}`
`" " = 14/3`
`" " ~~ 4.6667`