If sin=3/5 what is cos,tan,csc, sec,cot?

Question

201962 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-06T03:03:30

$color(brown)(csc theta = 5/3$

$color(blue)(cos theta = 4/5, sec theta = 5/4$

$color(green)(tan theta = 3 / 4, cot theta = 4/3$

![https://www.mathopenref.com/triangle345.html]
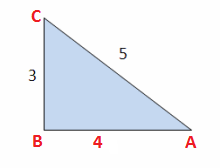( useruploads.socratic.org )

$sin theta = "(Oppo. side) /( Hypotenuse)" = 3 / 5$

According to Pythagorus Theorem,

$"Adj. side " AB = sqrt ((AC)^2 - (BC)^2) = sqrt (5^2 - 3^2) = 4$

Any triangle whose sides are in the ratio 3:4:5 is a right triangle.

Such triangles that have their sides in the ratio of whole numbers are called $color(red)("Pythagorean Triples."$

There are an infinite number of them, and this is just the smallest.

$csc theta = 1/ sin theta = 5/3$

$cos theta = (AB) / (AC) = 4/5$

$sec theta = 1 / cos theta = 5/4$

$tan theta = (BC) / (AB) = 3 / 4$

$cot theta = 1 / tan theta = 4/3$