If some galaxies in the local group exhibit blueshift spectral lines, why aren't these blueshifts violations of the Hubble's law?
1 Answer
Hubble's law is applicable only for fundamental observers . Fundamental observers are those who flow with the cosmic fluid. The blue shifted galaxies are not fundamental observers.
Explanation:
In an expanding Universe the physical distance between objects change. It is not that the objects move away from each other. What is happening is that the space between them expand while the objects stayed put. From the perspective of each observer they are fixed and everyone else is drifting away from them.
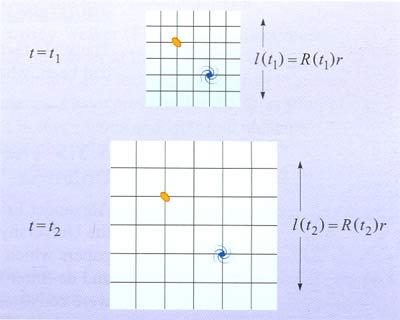
We can get a better understanding by drawing a grid system that co-expands with the Universe. This grid system is called the comoving coordinate system (See the attached Figure). Imagine galaxies located at grid points. If objects are merely moving because of the Hubble expansion, then the objects will remain at the same grid points at every instant of time, though the physical distance between them is increasing with time.
Fundamental observers are those whose comoving coordinates do not change as the Universe expand, which the physical distance between them change. Not all observers are fundamental observers. There could be motion other than the Hubble expansion, such as the motion due to strong gravitational interaction between objects (galactic collisions etc).
In general, for a isotropically expanding Universe, the physical distance between the objects can be written as :
The velocity of an object is :
The velocity of an object in an expanding Universe has two components.
The first term
The second term
For the fundamental observers the comoving distance
For non-fundamental observers the comoving distance
The blue shift you are talking about is due to peculiar velocity.