Question

If street lights are placed at most 132 feet apart, how many street lights will be needed for a street that is 4 miles long, assuming that there are lights at each side of the street?

Answer 1

If lights need to be placed across from each other down the street,
then at least `322` lights will be needed.

Explanation:

interpretation 1
"lights at each side of the street" means that lights are to be placed across from each other down the street.

In this case the number of lights needed will be twice the number of lights needed along one side of the street with a maximum of 132 feet between these lights.

`4 " miles" =4xx5280 " feet"`
and with `132" feet"` per interval between poles
we would need
`color(white)("XXX")(4xx 5280" feet")/(132" feet")`

`color(white)("XXX")=160` intervals between poles

Since we need to start with a pole (at distance `0`) and need `160` more poles
we will need `161` poles on each side of the street

or a total of `161xx2=322` poles for both sides of the street.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

interpretation 2
If we can alternate the poles on opposite sides of the street we can (probably) accomplish this with fewer poles.

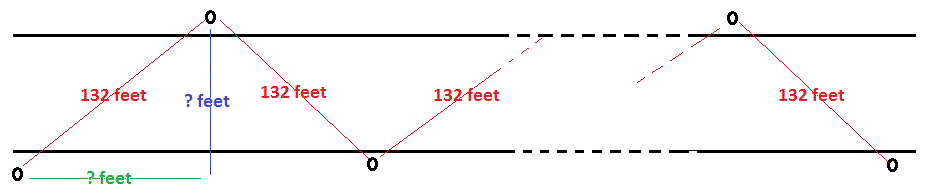
Without knowing the distance across the street we can not be sure of how many posts would be required.

For demonstration purposes if the `color(blue)("distance across the street")` was approximately `33` feet so that the component of the displacement between street lights in the direction of the street was `color(green)(128" feet")`

Then there would be
`color(white)("XXX")(5280xx4)/128 = 165` intervals
and
`color(white)("XXX")166` poles would be needed.