If the length of a #21 cm# spring increases to #45 cm# when a #2 kg# weight is hanging from it, what is the spring's constant?
1 Answer
Jan 8, 2017
I got
Explanation:
We can us Hooke's Law to relate the elastic force of a spring of elastic constant
Also, Newton's Second Law will help us to consider the forces involved through:
let us see:
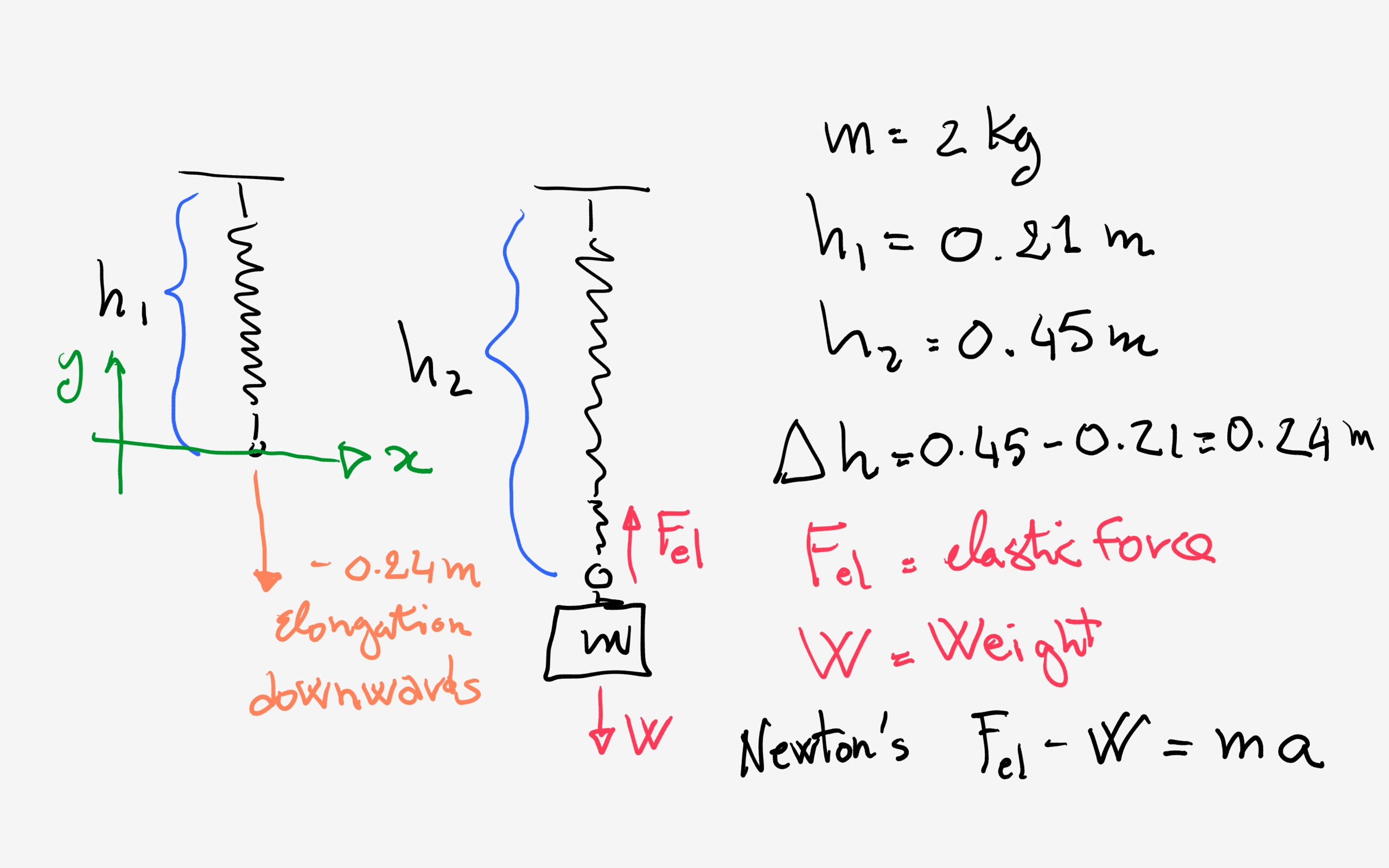
So at the equilibrium the elastic force and the weight (
But the elongation is directed downwards so we write, using numbers:
So:
I changed the lengths into meters because I am used to this but if you need it in N/cm use

