If the sum of the interior angles of a polygon is 720°, what type of polygon is it?
1 Answer
Please read the explanation.
Explanation:
Given:
Sum of the interior angles of a polygon is:
The relationship between the number of sides of a polygon and the sum of interior angles is
where
Hence, we have
Divide both sides of the equation by
Add
Hence, the required polygon must have 6 sides.
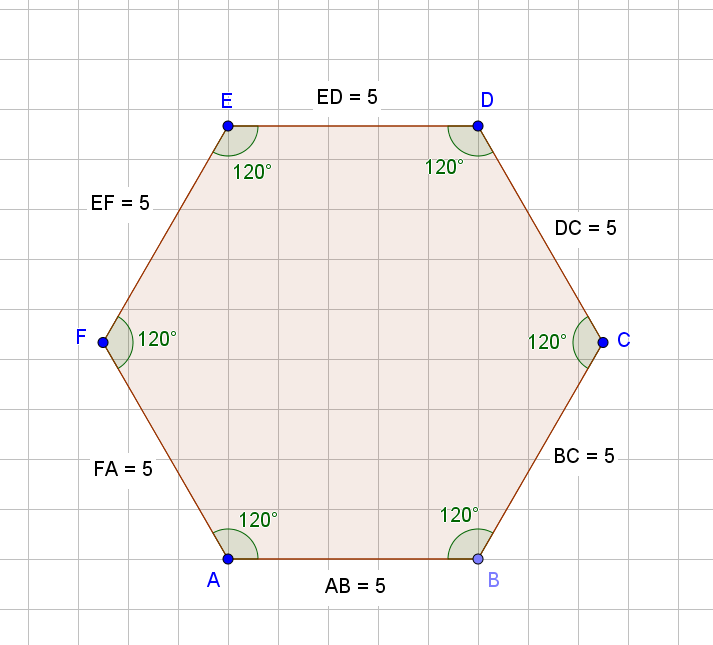
A Hexagon is a six-sided polygon.
Hence, the type of polygon required is a Hexagon.
If you are interested, you can find an image of a regular hexagon below:
Hope it helps.

