If the two reactions below are coupled to form a voltaic cell, how do you calculate the standard emf (electromagnetic force) representing a spontaneous reaction?
#Mg^(2+)(aq) + 2e^(-) -> Mg (s) " "E^@ = - "2.37 V"#
#Ag^+(aq) + e^(-) -> Ag (s)" "E^@ = + "0.7991V"#
1 Answer
Explanation:
Notice that the problem provides you with the standard reduction potentials,
#"Mg"_ ((aq))^(2+) + 2"e"^(-) rightleftharpoons "Mg"_ ((s))" "E^@ = -"2.37 V"#
#"Ag"_ ((aq))^(+) + "e"^(-) rightleftharpoons "Ag"_ ((s))" "color(white)(a)E^@ = +"0.7991 V"#
Now, take a look at the values of
This means that when you place a piece of magnesium metal in solution, it will form cations more readily than the standard hydrogen electrode.
On the other hand, for the reduction of silver cations to silver metal,
This means that you place a piece of silver metal in solution, it will form cations less readily than the standard hydrogen electrode.
Since the standard reduction potential for the magnesium cations is negative when compared with the standard reduction potential for the silver cations, which is positive, when you connect these two half-cells, the magnesium reduction equilibrium will move to the left
#"Mg"_ ((s))-> "Mg"_ ((aq))^(2+) + 2"e"^(-)#
In this case, magnesium metal is being oxidized to magnesium cations. Because the reaction has been reversed, you need to flip the value of
#E_"oxidation"^@ = -E^@ = -(-"2.37 V") = +"2.37 V"#
The silver reduction equilibrium will move to the right
#"Ag"_ ((aq))^(+) + "e"^(-) -> "Ag"_ ((s))#
In this case, silver cations are being reduced to silver metal
#E_"reduction"^@ = E^@ = +"0.7991 V"#
Now, in any redox reaction, the number of electrons lost in the oxidation half-reaction will be equal to the number of electrons gained in the reduction half-reaction.
In your case, you need to have
Keep in mind that the value of
The two half-reactions will thus be
#{("Mg"_ ((s))-> "Mg"_ ((aq))^(2+) + 2"e"^(-)" " " " " "color(white)(a)E_"oxidation"^@ = +"2.37 V"), ("Ag"_ ((aq))^(+) + "e"^(-) -> "Ag"_ ((s))" " | xx color(blue)(2)" "E_"reduction"^@ = +"0.7991 V") :}#
#color(white)(aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa)/color(white)(aaaaaaaaaaaaaaaaaaaaaa)#
#"Mg"_ ((s)) + 2"Ag"_ ((aq))^(+) + color(red)(cancel(color(black)(2"e"^(-)))) -> "Mg"_ ((aq))^(2+) + color(red)(cancel(color(black)(2"e"^(-)))) + 2"Ag"_ ((s))#
This is equivalent to
#"Mg"_ ((s)) + 2"Ag"_ ((aq))^(+) -> "Mg"_ ((aq))^(2+) + 2"Ag"_ ((s))#
Now, because the half-reactions are additive, so are the reduction and oxidation potentials. You can thus say that the standard cell potential,
#color(purple)(|bar(ul(color(black)(E_"cell"^@ = E_"reduction"^@ + E_"oxidation"^@)color(white)(a/a)|)))#
In your case, you will have
#E_"cell"^@ = +"0.7991 V" + "2.37 V" = color(green)(|bar(ul(color(white)(a/a)color(black)("3.17 V")color(white)(a/a)|)))#
The answer is rounded to two decimal places.
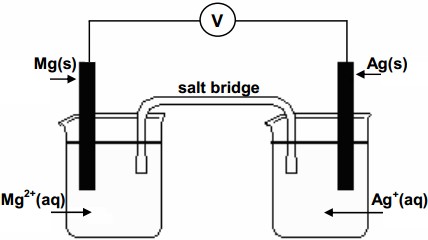
Here's how this cell would look like
In your case, the electrons will flow from the magnesium electrode, which acts as anode, i.e. here is where oxidation takes place, to the silver electrode, which acts as cathode, i.e. here is where reduction takes place.