If two chords AB and CD of a circle perpendicular to each other at point O then prove that # OA^2+OB^2+OC^2+OD^2=4R^2?#
2 Answers
Please see below.
Explanation:
Let us consider the chords
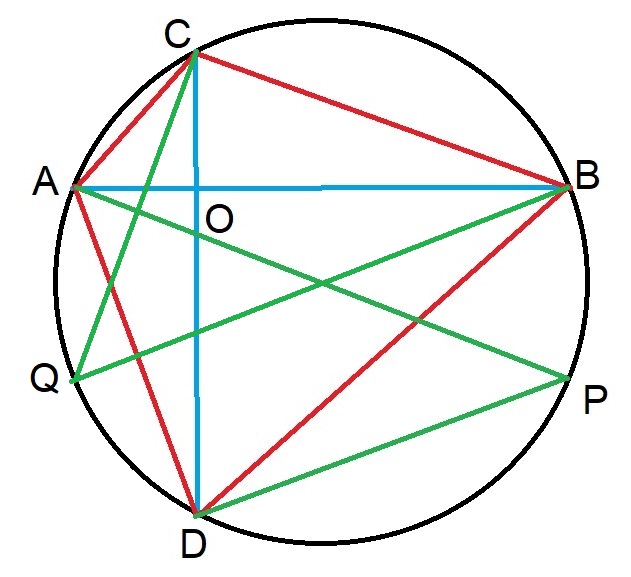
Now as
and as
i.e.
Now consider right angled
As
Hence
and hence
Similarly we can draw diameter
Hence,
=
=
Now in
and hence
=
=
=
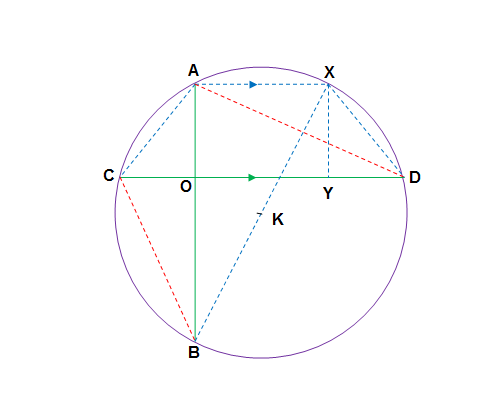
Let
If
#color (red)(OA^2+OB^2+OC^2+OD^2=4R^2)#
Constructions
As
Now
So
In
Hence
Now applying Pythagoras theorem for
#color (red)(=>OA^2+OB^2+OC^2+OD^2=4R^2)#
Proved

