Question

If two people pull on either side of the rope with a force of 65N, why is the tension in the rope 65N?

Answer 1

Apply Newton's third law. See below.

Explanation:

The rope experiences the same pulling force on both sides, and therefore it is in a state of static equilibrium (i.e. it is at rest consequently has a net force of zero).

A force diagram:

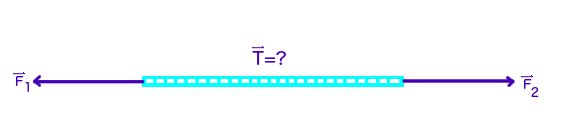
Where `vecF_1` and `vecF_2` are the pulling forces on the rope and `vecT` is the tension force. `R` will represent the rope later.

Here we consider Newton's third law.

Newton's third law states that every force occurs as a member of an action/reaction pair of forces. You may know it as the familiar phrase, "every action has an equal and opposite reaction." Most importantly, two members of an action/reaction pair are equal in magnitude but opposite in direction.

`vecF_(A on B)=-vecF_(B on A)`

In this situation, each person pulls on the rope with `65N` of force, so:

`vecF_(1 on R)=65N` and `vecF_(2 on R)=65N`.

This tells us that the pulling force exerted by each person on the rope is `65N`, and consequently by NIII, the rope exerts an equal but opposite tension force of `65N` on each person.

This is an action reaction pair. Therefore:

`vecF_(R on 2)=vecF_(2 on R)=vecF_(1 on R)=vecF_(R on 1)=65N`

The tension force in the rope, given by `vecF_(R on 1)` and `vecF_(R on 2)`, is therefore `65N`.