In a calorimeter, 1.0 kg of ice melts at 0°C. The enthalpy of fusion of the ice is 334 J/g. How much heat was absorbed?
1 Answer
Explanation:
A given substance's enthalpy of fusion,
It's important to remember that phase changes take place at constant temperature, which is why you'll sometimes see the enthalpy of fusion being referred to as the latent heat of fusion.
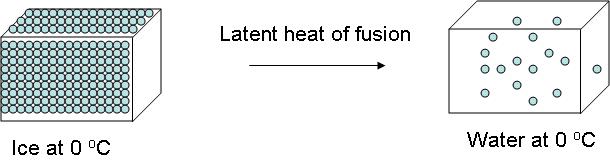
So, ice has an enthalpy of fusion equal to
To determine how much heat is needed to convert
First, convert the mass of the sample to grams by using the conversion factor
#"1 kg" = 10^3"g"#
This will get you
#1.0 color(red)(cancel(color(black)("kg"))) * (10^3"g")/(1color(red)(cancel(color(black)("kg")))) = 1.0 * 10^3"g"#
Use the mass of the sample and the enthalpy of fusion of ice to find
#1.0 * 10^3color(red)(cancel(color(black)("g"))) * overbrace("334 J"/(1color(red)(cancel(color(black)("g")))))^(color(purple)(DeltaH_"fus")) = 334 * 10^3"J"#
You need to round this off to two sig figs, the number of sig figs you have for the sample of ice. You can also express the result in kilojoules by using the conversion factor
#"1 kJ" = 10^3"J"#
The answer will thus be
#"heat absorbed" = color(green)(|bar(ul(color(white)(a/a)"330 kJ"color(white)(a/a)))|)#

