Question

In a circle of diameter `40` cm, the length of a chord is `20` cm. Find the length of minor arc of the chord?

Answer 1

I got `20.9cm`

Explanation:

Let us have a look at the diagram:

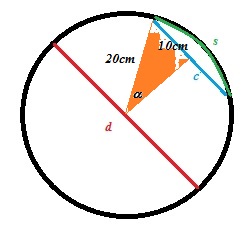
and consider the orange right triangle where the hypotenuse is equal to the radius `r=d/2=40/2=20cm` and one of the sides is half the length of the chord, `20/2=10cm`.
We can evaluate the angle `alpha` using trigonometry:

`10=20sin(alpha)`

`alpha=arcsin(10/20)=30^@`

so that the entire angle `theta` will be:

`theta=2alpha=60^@`
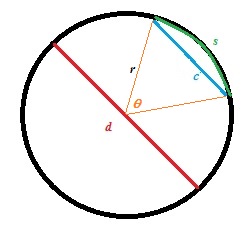
in radians this angle is: `pi/3`.

We can use this value in radians into:

`s=rtheta`

to find the length of the arc `s`:

`s=20pi/3=20.9cm`