In an isosceles trapezoid ABCD, AB=CD=5. The top base = 8 and the bottom base = 14. What is the area of this trapezoid?
3 Answers
The area is 44
Explanation:
We know that the area of any trapezoid is
To find the area we, therefore, only need to calculate h.
We can see from the figure that
(this follows from
Therefore
(The triplet 3,4,5 is a well known triplet for right triangles, but you also see it from
Therefore the area is
Explanation:
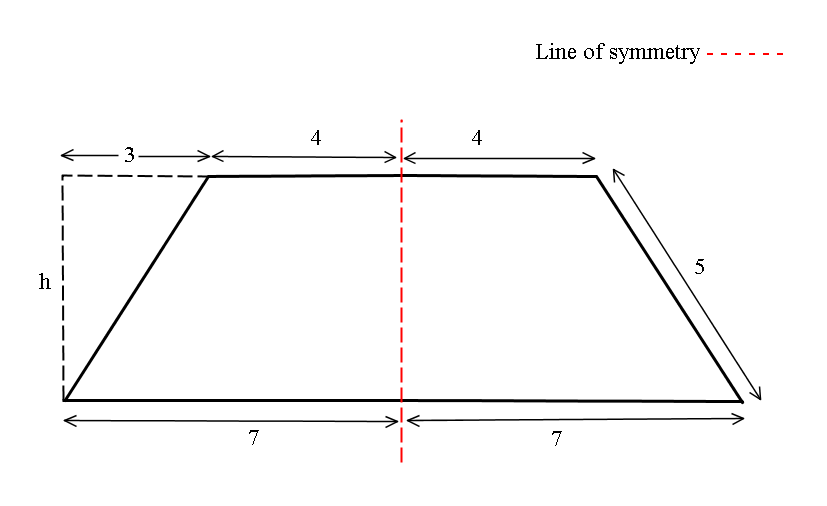
The area of a trapezoid is given as:
Where
From the diagram notice the line of symmetry is at the midpoints of the base and top, also notice that the triangle formed on the left has sides
The 3 is arrived at by noticing this is
We need to find h:
We know the hypotenuse of the triangle is 5, so by Pythagoras' theorem:
We can now calculate the area:
The area of the trapezoid is
Explanation:
I went ahead and drew the trapezoid:
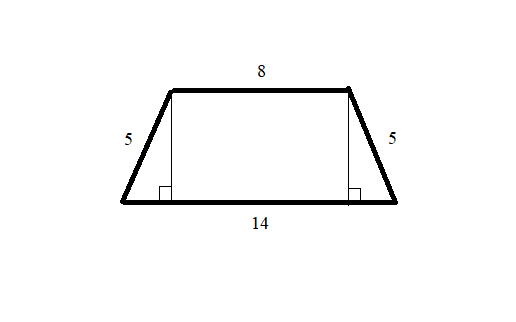
The area formula for a trapezoid is:
The measures of the two bases have been given, but the height has not been given. The height of the trapezoid can be found using the Pythagorean Theorem.
As you can see below, I drew the heights of the trapezoid on either side. I marked one as
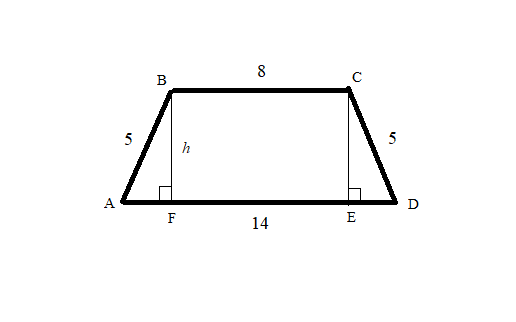
Before we can use the Pythagorean Theorem, the length of
#BC = FE = 8# [As#BCEF# is a parallelogram]#AF = ED# [As#DeltaAFB ~= DeltaCED# ]
Calculate
Now use
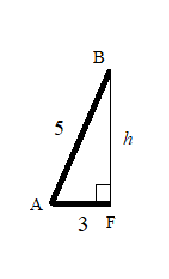
Now plug that into the original area formula:
The area of the trapezoid is



