Why is a trapezoid a quadrilateral, but a quadrilateral is not always a trapezoid?
1 Answer
Nov 12, 2015
When you consider the relationship between two shapes, it is useful to do so from both standpoints, i.e. necessary vs. sufficient.
Necessary -
Sufficient - The qualities of
Questions you might want to ask:
- Can a trapezoid exist without possessing the qualities of a quadrilateral?
- Are the qualities of a quadrilateral sufficient to describe a trapezoid?
Well, from these questions we have:
- No. A trapezoid is defined as a quadrilateral with two parallel sides. Therefore, the quality of "quadrilateral" is necessary, and this condition is satisfied.
- No. Any other shape can have four sides, but if it does not have (at least) two parallel sides, it cannot be a trapezoid. An easy counterexample is a boomerang, which has exactly four sides, but none of them are parallel. Therefore, the qualities of a quadrilateral do not sufficiently describe a trapezoid and this condition is not satisfied.
Some crazy examples of quadrilaterals:
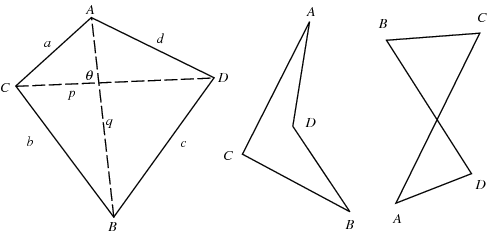
This means that a trapezoid is too specific of a quadrilateral that merely having the quality of "quadrilateral" does not guarantee the quality of "trapezoid".
Overall, a trapezoid is a quadilateral, but a quadrilateral doesn't have to be a trapezoid.

