Question

In `DeltaABC,/_BAC=30^@;/_ACB=60^@ and BC = 6 cm`. How will you find out the area of the triangle without using trigonometry?

Answer 1

`18sqrt3 cm^2`

Explanation:

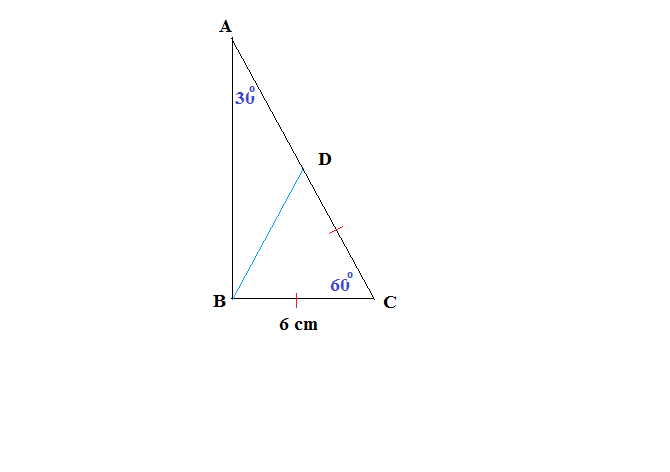
Given

• `"In " Delta ABC`

`->/_ACB=60^@`

`->/_BAC=30^@`

`->Rest/_ABC=90^@`

`-> and BC = 6 cm`

Construction

`CD = BC " is cut off from " CA " and B,D are joined"`

Analysis

`"In " Delta BDC`

`/_BCD=60^@,BC=CD->/_CDB=/_CBD=60^@`

`:. Delta BDC " is equilateral "->BC=CD=BD=6 cm`

`"In " Delta ABD`

`/_ABD=/_ABC-/_DBC=(90-60)=30^@`

`and /_BAD=30^@=>Delta ABD-> "isosceles triangle"`

`=>AD=BD=6 cm`

`"Now " AC = AD +CD =(6+6) cm=12 cm`

`" Now applying Pythagoras theorem for " Delta ABC`

`AB= sqrt(AC^2-BC^2)=sqrt(12^2-6^2)=6sqrt3 cm`

`" Area of " Delta ABC=1/2xxABxxBC=1/2*6sqrt3*6=18sqrt3 cm^2`