We can determine where a function is convex or concave, by using the second derivative. If:
#(d^2y)/(dx^2)f(x)>0color(white)(888)# Convex( concave up )
#(d^2y)/(dx^2)f(x)<0color(white)(888)# Concave( concave down )
The second derivative is just the derivative of the first derivative. .i.e.
#(d^2y)/(dx^2)f(x)=dy/dx(dy/dxf(x))#
For #f(x)=cos(x)#
#dy/dx=-sin(x)#
#(d^2y)/(dx^2)(cos(x))=dy/dx(-sin(x))=-cos(x)#
Now we solve the inequalities:
#-cos(x)>0color(white)(888)[1]#
#-cos(x)<0color(white)(888)[2]#
#-cos(x)>0color(white)(888)[1]#
#pi/2 < x< (3pi)/2#
#-cos(x)<0color(white)(888)[2]#
#0 < x < pi/2color(white)(88)# , #(3pi)/2 < x < 2pi #
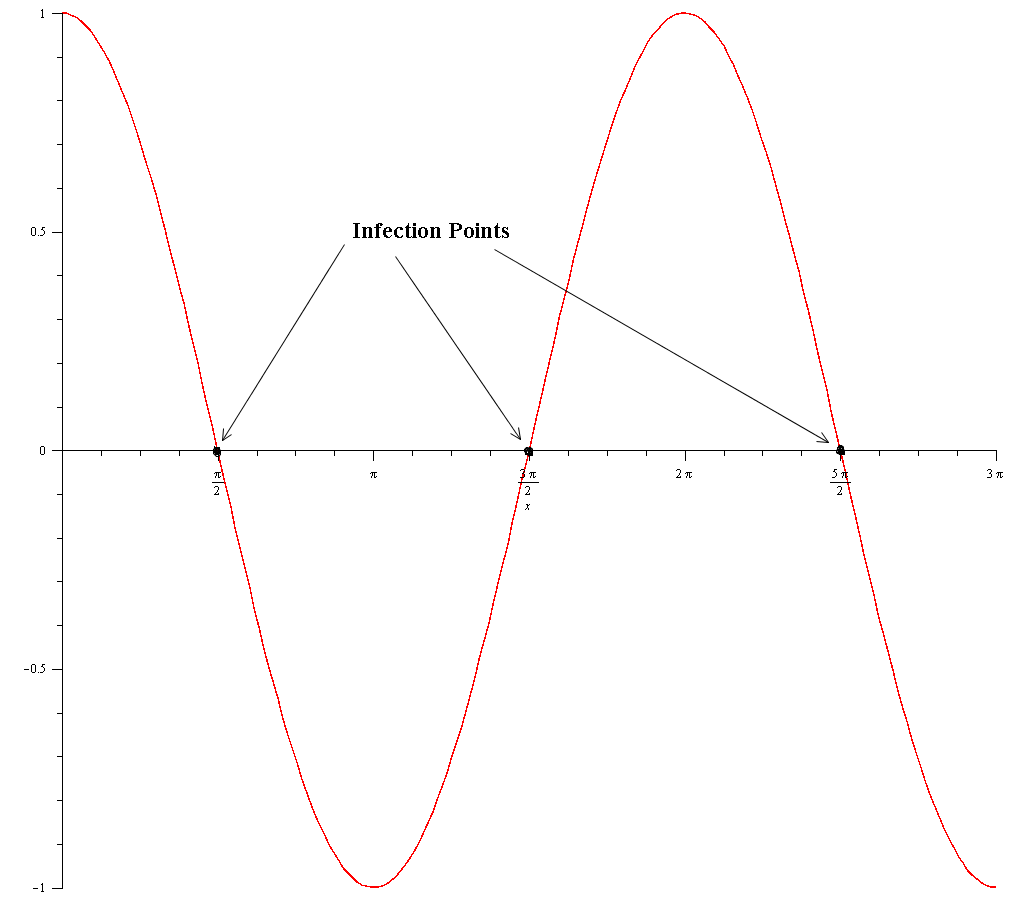
Notice that #bb((3pi)/2)# is on the point where the function changes from convex to concave. This is called a point of inflection ( inflexion in the UK ), so at #bb((3pi)/2)# it is neither concave nor convex.
This is verified by its graph: