# f(x) = cosx #
Differentiating wrt #x# we get
#f(x) = cosx => f'(x) = -sinx#
When #x=pi/2 => f'(pi/2)=-sin(pi/2) = -1 #
Now #{ (f'(x)<0, => f(x) " is decreasing"), (f'(x)=0, => f(x) " is stationary"), (f'(x)>0, => f(x) " is increasing") :}#
So we know that #f(x)# is decreasing at #x=pi/2#, we must check the 2nd derivative for the convexity
#f'(x) = -sinx => f''(x)=-cosx#
When #x=pi/2 => f''(pi/2)=-cos(pi/2) = 0 #
Now #{ (f''(x)<0, => f(x) " is concave"), (f''(x)=0, => f(x) " is transition point"), (f''(x)>0, => f(x) " is convex") :}#
Confirming that #x=pi/2# corresponds to a transition between convex down and convex up.
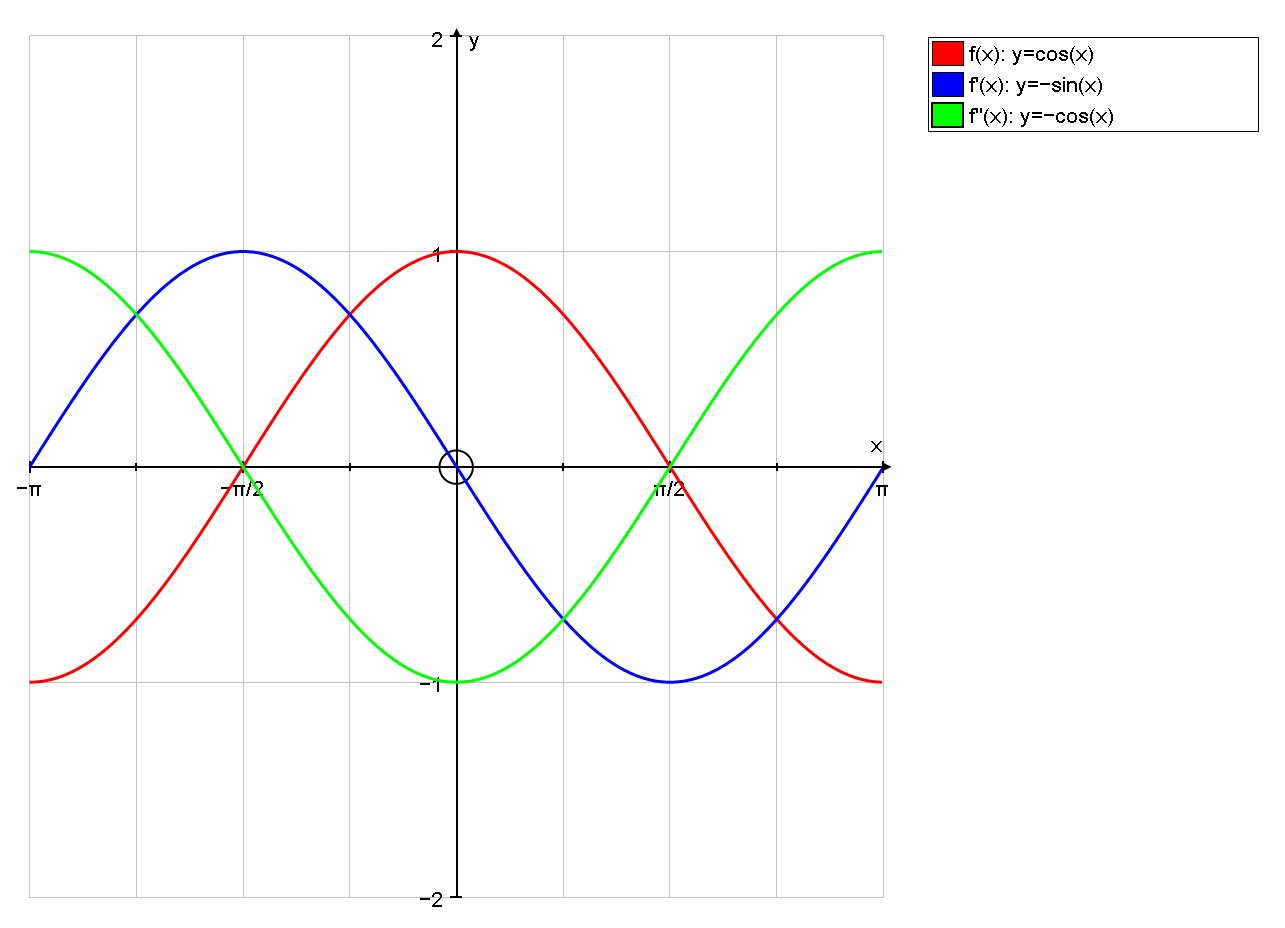
The following is a plot of #color(red)(f(x))#, #color(blue)(f'(x))# and #color(green)(f''(x))#. As you can see when #x=pi/2# then #color(red)(f(x))# is decreasing and #color(blue)(f'(x)) < 0#, and #color(green)(f''(x)) = 0#