Is it possible to solve for #u# and #v#, given the following matrix multiplication chain?
I am attempting to determine the intersections between a parametric Bezier surface, and line #L=P_0+tV# , where #P# is a point that lies on the line, and #V# is a vector describing the line's direction.
The following image's source presents a seemingly convenient matrix form. The equation in the image represents the calculation of a point that lies on the surface, given the parameters #u# and #v# .
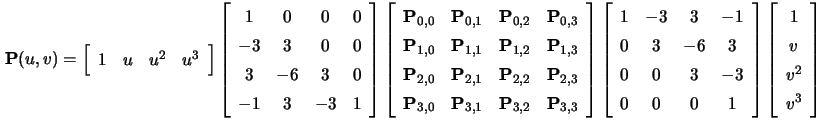
I figured the next logical step would be to substitute #P(u,v)# for the equation of the line given above, but I am unsure how to proceed.
I have tried to isolate the #u# and #v# coefficient matrices, but to no avail.
Is it possible to solve for #u# and #v# ? Are there any alternatives?
I am attempting to determine the intersections between a parametric Bezier surface, and line
The following image's source presents a seemingly convenient matrix form. The equation in the image represents the calculation of a point that lies on the surface, given the parameters
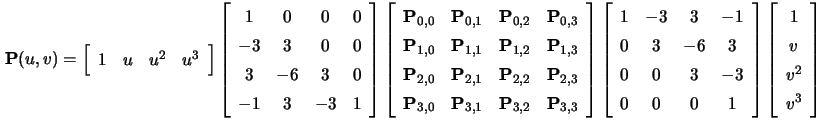
I figured the next logical step would be to substitute
I have tried to isolate the
Is it possible to solve for
1 Answer
See below.
Explanation:
After matrix multiplication we obtain
The line is defined as
The intersections are obtained solving
Three equations with three unknowns. The solutions can be obtained using an iterative procedure like Newton-Raphson.
where
Calling now
where
we have

