Is it true that for a value of #n# (n-principal quantum number), the value of #m_l# (#m_l#-magnetic quantum number) is equal to #n^2#? If it is true, can you please explain this to me? Thanks.
1 Answer
The actual value, no. The number of values, yes.
Explanation:
The relationship between the principal quantum number,
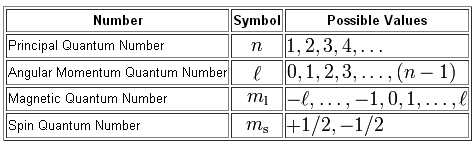
The angular momentum quantum number can take any value that ranges from
The magnetic quantum number can take any value that ranges from
If you take into account the possible values of
So, for example, if
and
As you can see, the individual values of
However, the total number of values
The magnetic quantum number actually tells you how many orbitals a subshell has. In the above example, if
This means that the second energy level has a total of two subshells, the 2s-subshell and the 2p-subshell.
The number of orbitals each subshell contains is given by
The 2p-subshell contains 3 orbitals, each denoted by a different value of
The total number of orbitals in the second energy level is 4, which is equal to
If you try this with
- one 3s-orbital;
- three 3p-orbitals;
- five 3d-orbitals.

