Is the dissociation energy of fluorine low?
1 Answer
tldr; Yes, it is, due to the electron/electron coulombic repulsions that dominate because of the exceptionally short bond of
Surprisingly, yes. Comparing it to the other halogens, we have:
It appears to be an anomaly in the pattern, where one might expect that due to the decreasing radii, the atoms are smaller and thus have shorter and stronger bonds at their equilibrium geometry. That is true to an extent.
BACKGROUND
Let us construct a simple equation relating the overall ground-state energy of a diatomic molecule as it varies according to bond distance.
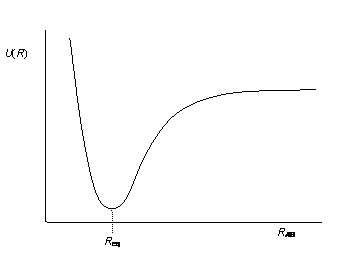
Recall that on a potential energy curve, you have this delicate balance between putting the atoms too close and too far away. When they're too close, you get significant nuclear repulsions. Otherwise, you either don't have strong enough orbital overlap or you do. If you do, you form the bond. Furthermore, we have coulombic repulsions that instantaneously occur between electron pairs. Thus, we have a term for all three interactions.
#E ~~ underbrace(E_"bond")_"dissociation/association" + underbrace(E_"pair")_"electron/electron repulsions" + underbrace(h_"nuc")_"nuclear repulsions"#
In essence, these terms are, respectively:
- The bond dissociation energy (or energy stored in the bond)
- The coulombic repulsion energy associated with electron pairs repelling each other instantaneously
- The potential energy associated with two nuclei repelling each other as they get too close (remember the left side of the potential energy curve you saw in General Chemistry?)
TAKE-HOME MESSAGE
Remember that the goal is to achieve a minimum energy.
The nuclei are so close together that we have a substantial electron/electron repulsion effect, since the valence electron clouds are the first to overlap as the nuclei approach each other. Remember, the atom is much larger than its nucleus.
Also, nuclear repulsions do destabilize the bond (remember, there are protons inside each nucleus). However, this is minor, and is secondary to the effect of the valence electron coulombic repulsions.
As both of the above effects increases in magnitude,
The decrease in the dissociation energy reflects the lower stability of the bond, thus saying that it is easier to break the

