Is #y= -4/x# a linear equation?
2 Answers
The given equation is not linear because the power of
Explanation:
Given -
#y=-4/x#
The given equation is not linear because the power of
#y=-4x^(-1)#
Look at this graph of the given equation.
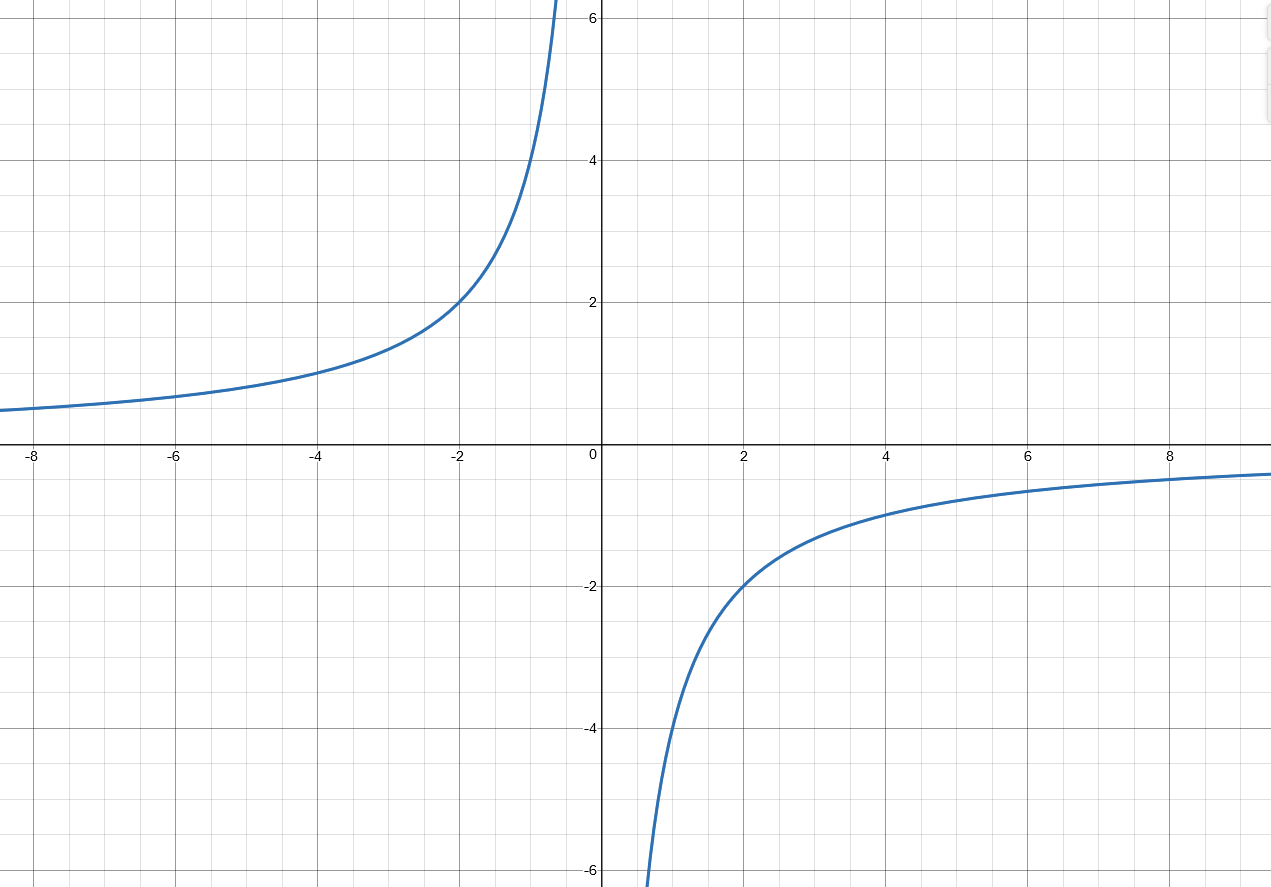
No.
It is a reciprocal equation.
Explanation:
Given:
Generate a data table as shown below:
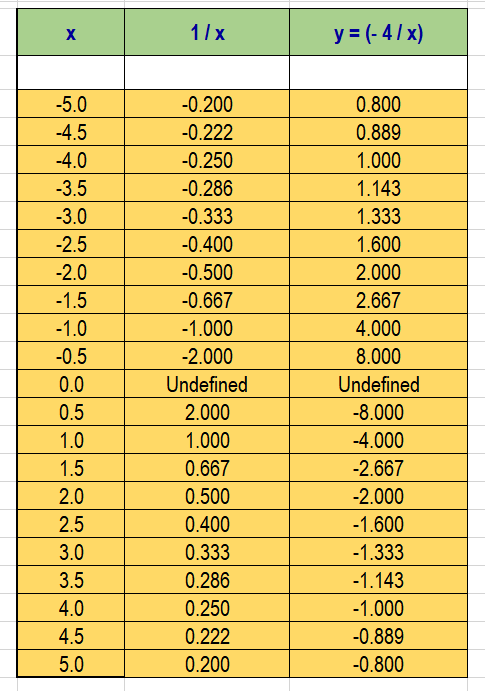
Display just the
Graph both the parent reciprocal function and the given function for the purpose of comparison:
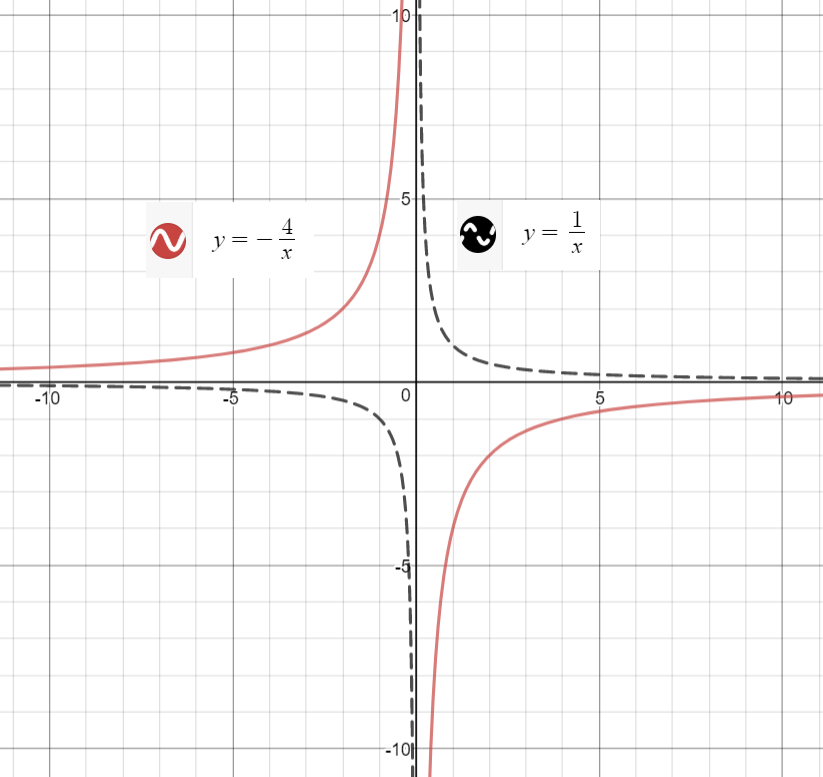
is a reciprocal function and it represents a hyperbola.
It is also an odd function.
The function's domain is all real values, except zero.
It is also very obvious, examining the graph:
For the parent function :
Horizontal and Vertical Asymptotes:
For the given function :
Horizontal and Vertical Asymptotes:
Hope it helps.


