Question

It has a triangle equal to 180 degrees and I don’t understand this, can you help me?

Answer 1

See below.

Explanation:

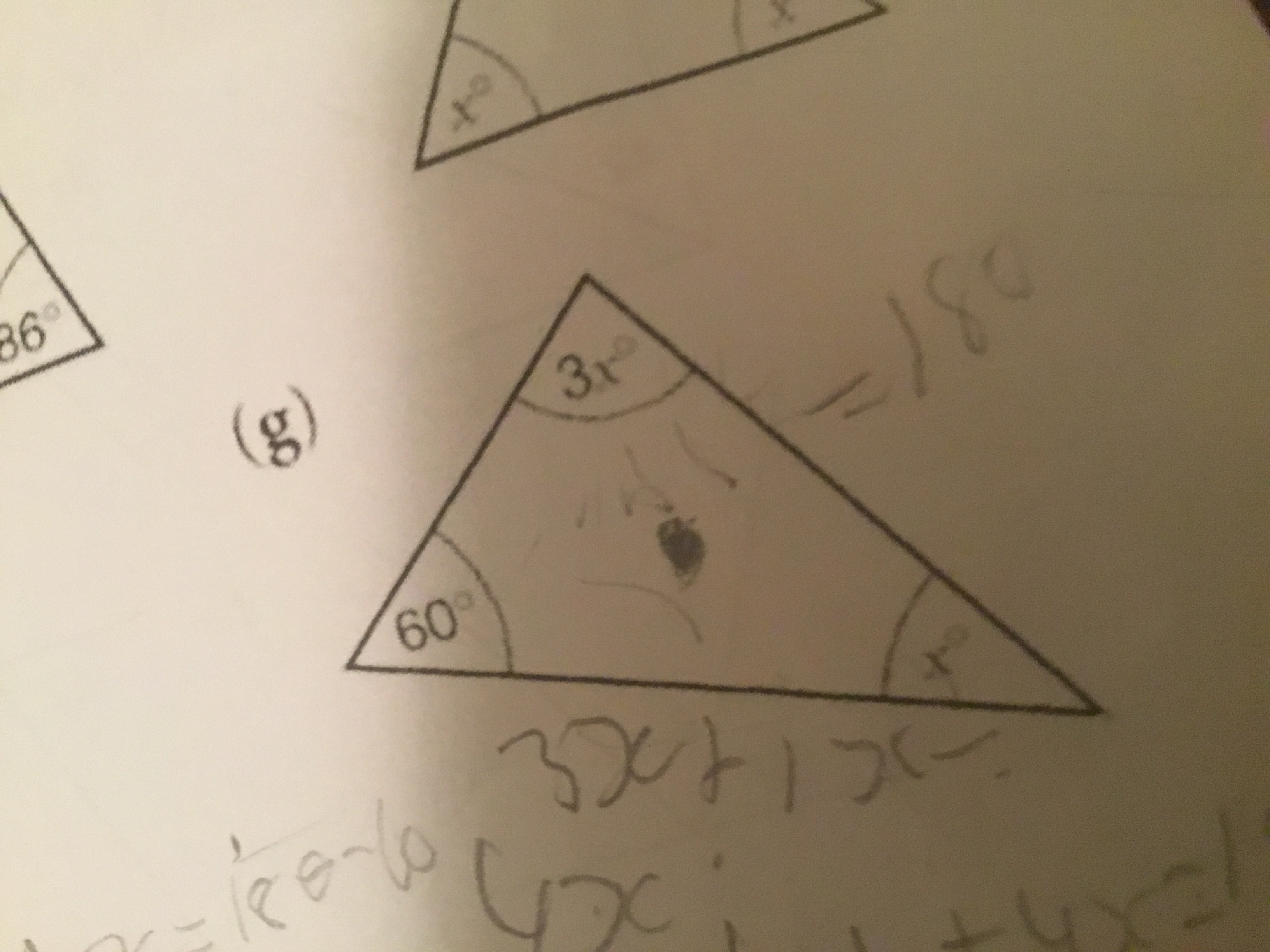
Here we are formulating an equation to solve for `x`.

We know that the interior angles of any triangle adds up `180` degrees.

We have three angles given:

`60`
`x`
`3x`

This means that :

`60+3x+x=180`

Now we collect like terms to simplify.

`60+4x=180`

Now we solve like any linear equation by isolating the variable on one side of the equation with the constant on the other.

Here we must subtract `60` from both sides to isolate the `x`.

`therefore 60 + 4x -60 = 180 -60`

`=>4x=120`
We want one `x`, therefore we divide by the coefficient of `x` on both sides.

Here we divide by `4`

`4x=120`
`=>x=30`

We can check if we are right by putting our value of `x` back into our formulated equation above.

`60 + (4*30) = 60+120 = 180`

Answer 2

Triangle sum theorem states that all angles in a triangle must add up to `180^@`, a similar theorem applies to quadrilaterals and it states that all angles in a quad. must add up to `360^@`.

Explanation:

You have already applied the triangle sum theorem which states that all 3 angles in a triangle add up to `180` degrees it seems, so now all you have to do is create an algebraic expression that reflects that.

`"Angle 1 + Angle 2 + Angle 3" = 180^@`

`x+3x+60=180`

`4x+60=180`

`4x=120`

So

`x= 30^@`

The angle `x` is 30 degrees and the angle `3x` is `90` degrees