Question

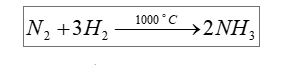
If `K_p = 2.4 * 10^(-3)` for the reaction below, then what is `K_c` ?

Answer 1

`K_c = 26`

Explanation:

Your tool of choice here will be the equation

`color(blue)(ul(color(black)(K_p = K_c * (RT)^(Deltan))))`

Here

• `K_p` is the equilibrium constant in terms of partial pressures
• `K_c` is the equilibrium constant in terms of concentrations
• `R` is the universal gas constant, equal to `0.0821 quad ("atm" * "L")/("mol" * "K")`
• `T` is the absolute temperature at which the reaction takes place
• `Deltan` is the difference between the number of moles of gaseous products and the number of moles of gaseous reactants

Now, your reaction takes place at `1000^@"C"`, so start by converting the temperature from degrees Celsius to Kelvin.

`T = 1000^@"C" + 273.15 = "1273.15 K"`

Notice that for every `1` mole of nitrogen gas that takes part in the reaction, the reaction consumes `3` moles of hydrogen gas and produces `2` moles of ammonia.

This means that you have

`Deltan = color(white)(overbrace(color(black)(" 2 "))^(color(blue)("moles of ammonia")) " "color(black)(-)" " overbrace(color(black)((" 1 + 3 ")))^(color(blue)("moles of reactants"))`

`Deltan = - 2`

Rearrange the equation to solve for `K_c`

`K_c = K_p/((RT)^(Deltan)`

Plug in your values to find--since you didn't provide any units for `K_p`, I'll do the calculation without added units!

`K_c = (2.4 * 10^(-3))/(0.0821 * 1273.15)^(-2) = color(darkgreen)(ul(color(black)(26)))`

The answer is rounded to two sig figs, the number of sig figs you have for `K_p`.