Label the orbital with the following quantum numbers?
1)n=5 l=0
2)n=4 l=2
3)n=2 l=1
4)n=3 l=0
5)n=6 l=2
6)n=7 l=1
1)n=5 l=0
2)n=4 l=2
3)n=2 l=1
4)n=3 l=0
5)n=6 l=2
6)n=7 l=1
1 Answer
Here's what I got.
Explanation:
If I understand your question correctly, you need to take those pairs of quantum numbers and specify the orbital that matches those values.
The problem with that lies with the fact that specific orbitals are determined by the value of the magnetic quantum number,
So I assume that you have to name all the orbitals that can share each of those pairs of quantum numbers.
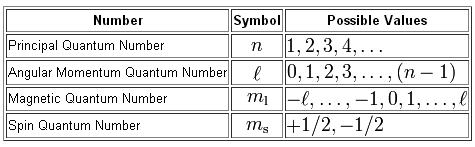
Now, the principal quantum number,
The angular momentum quantum number,
#l=0 -># the s-subshell#l=1 -># the p-subshell#l=2 -># the d-subshell#l=3 -># the f-subshell
Now, the number of orbitals each subshell can hold depends on the possible values of
Without the value of
For example, the fist pair has
In this particular case,
I'll show you the next two pairs, so that you can solve the last three pairs as practice.
For
More specifically, this electron will reside in the 4d-subshell, since it has
#m_l = -2 -># this is the#4d_(x^2-y^2)# orbital#m_l = -1 -># this is the#4d_z^2# orbital#m_l = 0 -># this is the#4d_(xy)# orbital#m_l = 1 -># this is the#4d_(xz)# orbital#m_l = 2 -># this is the#4d_(yz)# orbital
Therefore, a total of five orbitals can share the quantum nubmers
Finally, for
The values of
#m_l = -1 -># this is the#2p_x# orbital*#m_l = 0 -># this is the#2p_y# orbital#m_l = 1 -># this is the#2p_z# orbital
Therefore, a total of three orbitals can share the quantum numbers

