Let R be the region in the first quadrant enclosed by the lines #x=ln 3# and #y=1# and the graph of #y=e^(x/2)#, how do you find the volume of the solid generated when R is revolved about the line y=-1?

Question

9040 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-07T12:23:21

# V = pi( -2 + 4 sqrt 3 - 3 ln 3 ) #

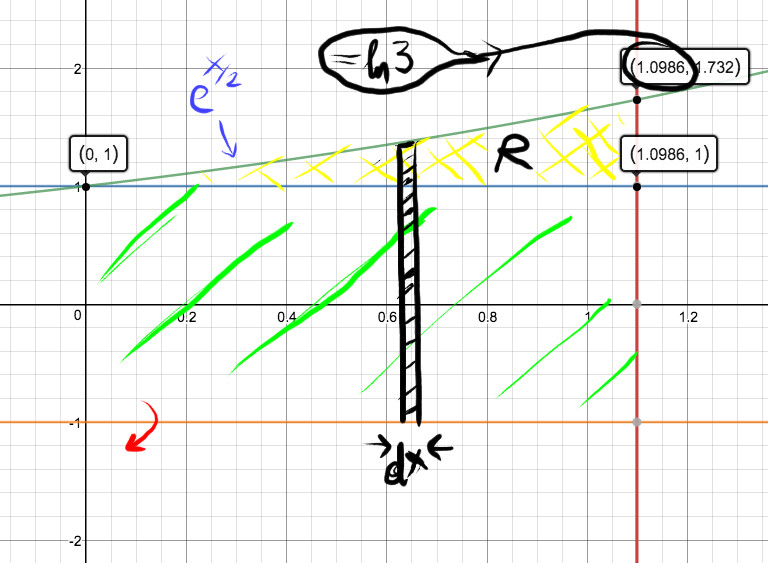
enter image source here

Easiest is to revolve #e^{x/2}# about y = -1 and then deduct the cylinder (shaded green) which has volume #pi * 2^2 * ln 3 = 4 pi ln 3#

So the volume of the small strip width dx when #e^{x/2}# is revolved about y = -1 is

#dV = pi (e^{x/2} + 1)^2 dx#

#V = pi int_0^{ln 3} dx qquad (e^{x/2} + 1)^2 #

# = pi int_0^{ln 3} dx qquad e^{x} + 2 e^{x/2} + 1 #

# pi [e^{x} + 4 e^{x/2} + x ]_0^{ln 3}#

# pi( [3 + 4 sqrt 3 + ln 3 ] - [1 + 4 + 0] )#

# pi( -2 + 4 sqrt 3 + ln 3 ) #

Then deducting the cylinder (shaded green) which has volume #= 4 pi ln 3#:

# V = pi( -2 + 4 sqrt 3 - 3 ln 3 ) #