Question

Let S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If `a,b,c and d` denote the lengths of sides of the quadrilateral, prove that `2<=a^2+b^2+c^2+d^2<=4`?

Answer 1

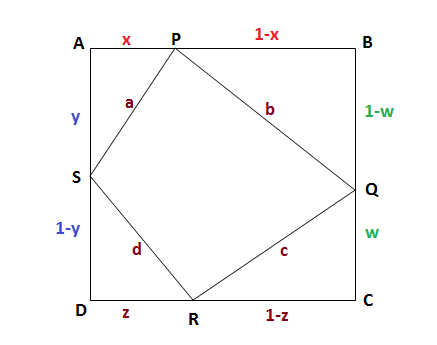
Let `ABCD` be a square of unit area.

So `AB=BC=CD=DA=1` unit.

Let `PQRS` be a quadrilateral which has one vertex on each side of the square. Here let `PQ=b,QR=c,RS=dandSP=a`

Applying Pythagoras thorem we can write

`a^2+b^2+c^2+d^2`

`=x^2+y^2+(1-x)^2+(1-w)^2+w^2+(1-z)^2+z^2+(1-y)^2`

`=4+2(x^2+y^2+z^2+w^2-x-y-z-w)`

`=2+2(1+x^2+y^2+z^2+w^2-x-y-z-w)`

`=2+2((x-1/2)^2+(y-1/2)^2+(z-1/2)^2+(w-1/2)^2)`

Now by the problem we have

`0<= x<=1=> 0<=(x-1/2)^2<=1/4`

`0<= y<=1=> 0<=(y-1/2)^2<=1/4`

`0<=z<=1=> 0<=(z-1/2)^2<=1/4`

`0<= w<=1=> 0<=(w-1/2)^2<=1/4`

Hence

`2<=a^2+b^2+c^2+d^2<=4`