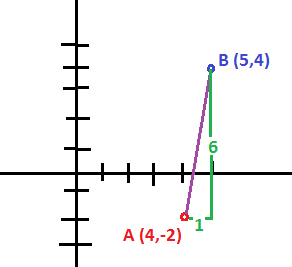
Objects A and B are at the origin. If object A moves to #(4 ,-2 )# and object B moves to #(5 ,4 )# over #8 s#, what is the relative velocity of object B from the perspective of object A? Assume that all units are denominated in meters.
1 Answer
Sep 26, 2016
Velocity:
Explanation:
Note that it doesn't matter that
The initial distance between
The distance between
Since this is the change in position relative to each other
the relative speed of
The tan of the angle (relative to the horizontal/X-axis) is
Therefore the angular component of the velocity is